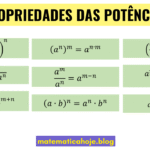
Propriedades da Potenciação
Guia completo: entenda as regras, veja exemplos resolvidos e pratique com exercícios.

Definição: Para um número real \(a\) e um número natural \(n\), a potência é definida como:
\[
a^{n} = \underbrace{a \cdot a \cdot a \cdots a}_{n\ \text{vezes}}
\]
A base é \(a\) e o expoente é \(n\).
1) Produto de potências de mesma base
\[ a^{m}\cdot a^{n}=a^{m+n} \]
Exemplo: \(3^{4}\cdot 3^{2}=3^{6}=729\).
2) Quociente de potências de mesma base
\[ \dfrac{a^{m}}{a^{n}}=a^{m-n}, \quad a\neq0 \]
Exemplo: \(\dfrac{4^{5}}{4^{3}}=4^{2}=16\).
3) Potência de potência
\[ (a^{m})^{n}=a^{m\cdot n} \]
Exemplo: \((6^{2})^{3}=6^{6}=46\,656\).
4) Potência de um produto
\[ (ab)^{n}=a^{n}\cdot b^{n} \]
Exemplo: \((5\cdot4)^{3}=5^{3}\cdot4^{3}=125\cdot64=8\,000\).
5) Potência de um quociente
\[ \left(\dfrac{a}{b}\right)^{n}=\dfrac{a^{n}}{b^{n}}, \quad b\neq0 \]
Exemplo: \(\left(\dfrac{2}{3}\right)^{3}=\dfrac{8}{27}\).
6) Expoente zero
\[ a^{0}=1, \quad a\neq0 \]
Exemplo: \(7^{0}=1\).
7) Expoente 1
\[ a^{1}=a \]
Exemplo: \(12^{1}=12\).
8) Expoente negativo
\[ a^{-n}=\dfrac{1}{a^{n}}, \quad a\neq0 \]
Exemplo: \(5^{-3}=\dfrac{1}{125}\).
9) Expoente fracionário
\[ a^{\tfrac{m}{n}}=\sqrt[n]{a^{m}}, \quad a\ge0 \text{ se }n\text{ par} \]
Exemplo: \(27^{\tfrac{2}{3}}=\left(\sqrt[3]{27}\right)^{2}=3^{2}=9\).
📘 Quer todas as fórmulas organizadas?
Baixe grátis o eBook Fórmulas Matemática
Baixe grátis o eBook Fórmulas Matemática
Exemplos resolvidos
Exemplo 1: Simplifique \( \dfrac{3^{8}\cdot3^{-2}}{3^{5}} \).
\[
\dfrac{3^{8-2}}{3^{5}}=\dfrac{3^{6}}{3^{5}}=3^{1}=3
\]
Exemplo 2: Resolva \( (4^{3/2})\cdot(4^{-1/2}) \).
\[
4^{3/2-1/2}=4^{2/2}=4^{1}=4
\]
Exemplo 3: Resolva \( 5^{2x-1}=\dfrac{125}{25} \).
\[
\dfrac{125}{25}=\dfrac{5^{3}}{5^{2}}=5^{1} \quad \Rightarrow \quad 5^{2x-1}=5^{1} \quad \Rightarrow \quad 2x-1=1 \quad \Rightarrow \quad x=1
\]
Erros comuns
- \((a+b)^{n}\neq a^{n}+b^{n}\).
- \(-3^{2}=-9\), mas \((-3)^{2}=+9\).
- Para expoentes fracionários com índice par: \(a\ge0\).
Exercícios (múltipla escolha)
1. Simplifique \( \dfrac{2^{7}\cdot2^{-3}}{2^{2}} \).
- a) \(2^{2}\)
- b) \(2^{3}\)
- c) \(2^{4}\)
- d) \(2^{5}\)
\[
2^{7-3-2}=2^{2}
\]
Resposta: (a)
2. \((9^{1/2})^{3} =\) ?
- a) 27
- b) 9√9
- c) \(3^{3}\)
- d) \(\sqrt[3]{9^{2}}\)
\[
(9^{1/2})^{3}=9^{3/2}=(\sqrt{9})^{3}=3^{3}=27
\]
Resposta: (a)
3. Resolva \(4^{x}\cdot2^{3}=2^{9}\).
\[
4^{x}=(2^{2})^{x}=2^{2x} \quad \Rightarrow \quad 2^{2x}\cdot2^{3}=2^{9}\quad \Rightarrow \quad 2x+3=9 \quad \Rightarrow \quad x=3
\]