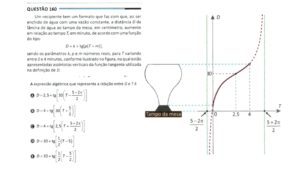
m quadrilátero é considerado circunscrito em uma circunferência se todos os seus lados são tangentes a uma circunferência. Nesse contexto, uma das propriedades mais importantes é a relação entre os comprimentos dos lados opostos do quadrilátero. Neste artigo, exploraremos essa relação fundamental e sua implicação para os quadriláteros circunscritos.
Propriedade dos Lados Opostos
Para um quadrilátero circunscrito, a soma dos comprimentos dos lados opostos é sempre igual. Isso é formalizado pelo Teorema de Pitot, que estabelece a seguinte relação para um quadrilátero circunscrito:
- Seja aaa, bbb, ccc e ddd os comprimentos dos lados do quadrilátero, em ordem consecutiva.
- O Teorema de Pitot afirma que:
a+c=b+d
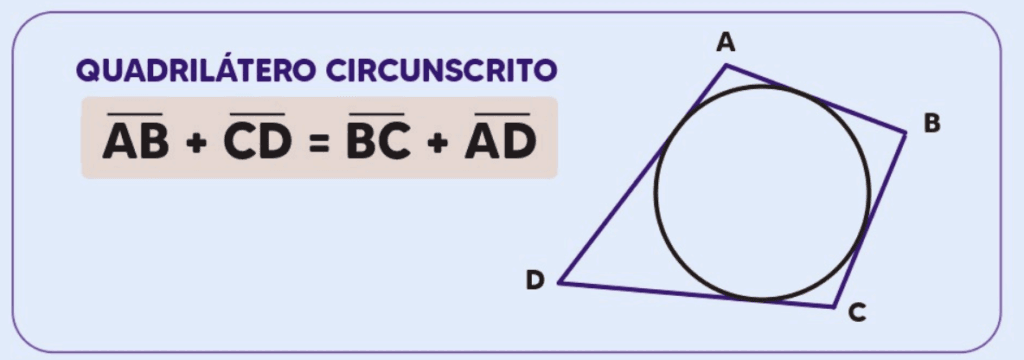
Esta propriedade é fundamental para a identificação e análise de quadriláteros que podem ser circunscritos em uma circunferência.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Exercícios Quadriláteros Circunscritos
1 – Vamos determinar o valor de x na figura envolvendo um quadrilátero circunscrito a uma circunferência.
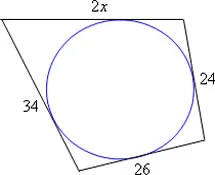
2x + 26 = 34 + 24
2x = 34 + 24 – 26
2x = 58 – 26
2x = 32
x = 32/2
x = 16
2 – Determine a medida dos lados do quadrilátero circunscrito à circunferência de acordo com a figura a seguir.
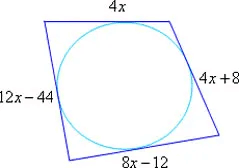
4x + 8x – 12 = 12x – 44 + 4x + 8
4x + 8x – 12x – 4x = – 44 + 8 + 12
– 4x = – 24
4x = 24
x = 24/4
x = 6
4x = 4 * 6 = 24
8x – 12 = 8 * 6 – 12 = 48 – 12 = 36
12x – 44 = 12 * 6 – 44 = 72 – 44 = 28
4x + 8 = 4 * 6 + 8 = 24 + 8 = 32
Soma dos Ângulos Opostos: Para um quadrilátero circunscrito, a soma dos ângulos opostos é sempre 180 graus. Ou seja, se AAA, BBB, CCC e DDD são os ângulos internos do quadrilátero, então:
A+C=180°
B+D=180°
3 – Determine o valor de α no quadrilátero abaixo.
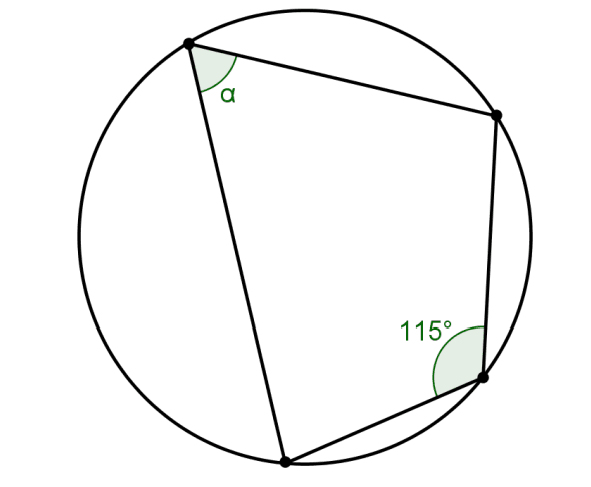
Solução: . Como o quadrilátero é inscritível, então a soma dos ângulos
opostos e 180°, ou seja, α = 180° − 115° = 65°
4 – Determine o valor de x no quadrilatero abaixo.
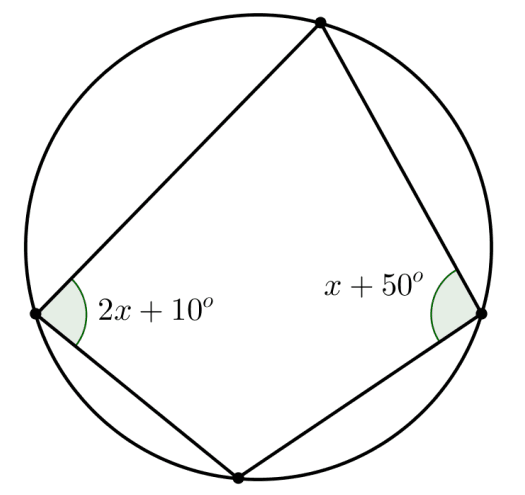
Solução: Como a soma dos ângulos opostos é 180°, pois o quadrilátero é inscritível, temos 2x + 10° + x + 50° = 180° , segue que x = 40°
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes