Questão 10
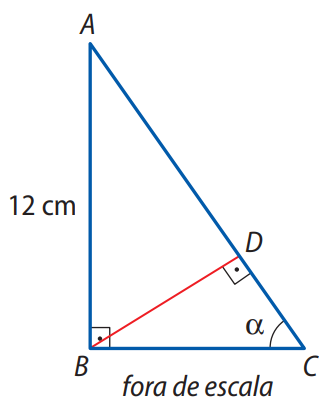
Enunciado: (UEA-AM) A figura mostra os triângulos retângulos \(ABC\) e \(BCD\), em que \(AB = 12 \, \text{cm}\) e \(\angle B\hat{C}D = \alpha\). Sabendo que \(sen \alpha = 0,8\) e que o ponto \(D\) está sobre o lado \(AC\), determine a medida do segmento \(DC\).
Alternativas:
- a) 5,4 cm
- b) 3,6 cm
- c) 4,5 cm
- d) 6,3 cm
- e) 7,2 cm
Solução Passo a Passo:
1. Determinar \(AC\) usando o seno:
\(sen \alpha = \frac{12}{AC} \Rightarrow 0,8 = \frac{12}{AC} \Rightarrow AC = \frac{12}{0,8} = 15 \, \text{cm}\)
2. Determinar \(BC\) usando Pitágoras no triângulo \(ABC\):
\(BC = \sqrt{AC^2 – AB^2} = \sqrt{15^2 – 12^2} = \sqrt{225 – 144} = \sqrt{81} = 9 \, \text{cm}\)
3. Determinar \(BD\) usando seno no triângulo \(BDC\):
\(sen \alpha = \frac{BD}{BC} \Rightarrow 0,8 = \frac{BD}{9} \Rightarrow BD = 0,8 \cdot 9 = 7,2 \, \text{cm}\)
4. Determinar \(DC\) com Pitágoras no triângulo \(BDC\):
\(DC = \sqrt{BC^2 – BD^2} = \sqrt{9^2 – 7,2^2} = \sqrt{81 – 51,84} = \sqrt{29,16} \approx 5,4 \, \text{cm}\)
Resposta: Alternativa a) 5,4 cm.
🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática
Explore Mais Conteúdos de Trigonometria
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon












