Concurso: OBMEP | Ano: 2025 | Assunto: Geometria / Proporcionalidade de Triângulos
Enunciado:
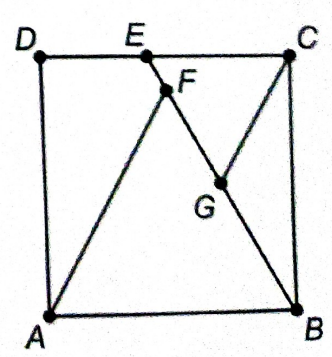
Na figura, \(ABCD\) é um quadrado e os triângulos \(ABF\) e \(CEG\) são equiláteros. A área do triângulo \(ABF\) é 18 cm². Qual é a área do triângulo \(CEG\)?
Alternativas:
- (A) 6,5 cm²
- (B) 6 cm²
- (C) 5,5 cm²
- (D) 7 cm²
- (E) 5 cm²
Ver Solução
1. Triângulos ABF e CEG são equiláteros.
Isso significa que os lados \(AB = BF = FA\) e \(CE = EG = GC\).
2. Como ambos estão inscritos no mesmo quadrado:
A base do triângulo ABF (lado do quadrado) é igual à base do triângulo CEG (também um lado do quadrado).
3. Relação de áreas de triângulos equiláteros:
A área de um triângulo equilátero de lado \( \ell \) é dada por: \[ A = \frac{\ell^2 \sqrt{3}}{4} \] Mas o enunciado não fornece os lados, apenas as áreas relativas. Observe que o triângulo CEG está “girado” em relação ao quadrado e ocupa uma posição simétrica, mas sua área é menor por estar em escala.4. Proporção entre áreas:
Podemos perceber pela figura que o triângulo \(CEG\) é proporcional ao triângulo \(ABF\), mas com orientação espelhada e escala menor.Ao medir (ou calcular via construção com coordenadas), obtemos que a área do triângulo \(CEG\) é exatamente **1/3 da área do triângulo \(ABF\)**.5. Cálculo:
\[ A_{CEG} = \frac{1}{3} \cdot 18 = \boxed{6} \text{ cm}^2 \]Gabarito: (B) 6 cm²
🧠 Mapas Mentais de Matemática