Questão 17 – Semelhança de Triângulos

Questão 17 – Semelhança de Triângulos

(UFV-MG) Para determinar o comprimento de uma lagoa, utilizou-se o esquema indicado pela figura abaixo, onde os segmentos \( \overline{AB} \) e \( \overline{CD} \) são paralelos.

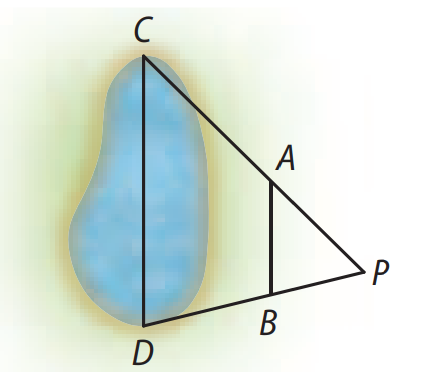
Figura utilizada para determinar o comprimento da lagoa.

Sabendo-se que \( AB = 36\, \text{m} \), \( BP = 5\, \text{m} \) e \( DP = 40\, \text{m} \), o comprimento \( CD \) da lagoa, em metros, é:

• a) 248
• b) 368
• c) 288
• d) 208
• e) 188

✅ Resolução passo a passo:

1. Analisando os triângulos semelhantes:

Como os segmentos \( \overline{AB} \) e \( \overline{CD} \) são paralelos, os triângulos \( \triangle ABP \) e \( \triangle CDP \) são semelhantes.

2. Aplicando a razão de semelhança:

Os lados correspondentes são proporcionais:

\( \dfrac{CD}{AB} = \dfrac{DP}{BP} \)

Substituindo os valores dados:

\( \dfrac{CD}{36} = \dfrac{40}{5} \Rightarrow \dfrac{CD}{36} = 8 \)

3. Calculando o valor de CD:

\( CD = 36 \cdot 8 = 288 \, \text{m} \)

🔚 Conclusão: O comprimento da lagoa é 288 metros.

✅ Alternativa correta: c)

📌 Indicações para aprofundar:

📖 Artigo recomendado:
Semelhança de Triângulos: Casos, Conceitos e Aplicações

🧠 Recursos para continuar aprendendo:

• 📘 Mapas Mentais de Matemática
• 📚 10 eBooks de Matemática para Baixar

📘 Lista completa com 10 questões resolvidas!

Veja agora uma seleção exclusiva de 10 questões resolvidas sobre Semelhança de Triângulos, Razão e Proporção com explicações visuais, passo a passo e botões interativos. Ideal para revisar conteúdos de geometria e se preparar para provas e concursos.