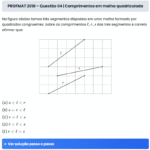
Considere as seguintes afirmações falsas:
I – Para todo número real \( \alpha \), se \( \alpha^2 = 1 \) então \( \alpha = 1 \).
II – Para quaisquer números reais \( x \) e \( y \) tem-se que \( x > y \implies x^2 > y^2 \).
Assinale a alternativa que contém contraexemplos para cada uma delas.
(B) \( \alpha = -1, x = -1, y = -2 \)
(C) \( \alpha = -\frac{1}{2}, x = -1, y = -2 \)
(D) \( \alpha = -1, x = 5, y = 2 \)
(E) \( \alpha = 1, x = -3, y = -5 \)
Resposta correta: (B)
1º Passo: Analisar a afirmação I.
Se \( \alpha^2 = 1 \), então \( \alpha = \pm 1 \). Para ser contraexemplo, basta \( \alpha = -1 \), pois satisfaz a hipótese mas não a conclusão.
2º Passo: Analisar a afirmação II.
Escolhendo \( x = -1 \) e \( y = -2 \), temos \( x>y \) mas \( x^2=1 < 4=y^2 \), portanto é contraexemplo para II.
✅ Logo, a alternativa B fornece contraexemplos para I e II simultaneamente.
🔗 Continue seus estudos: