PROFMAT 2025 – Questão 4 | Função Quadrática e Afim
Observe o sistema de coordenadas abaixo em que estão representados os gráficos de uma função afim e de uma função quadrática:
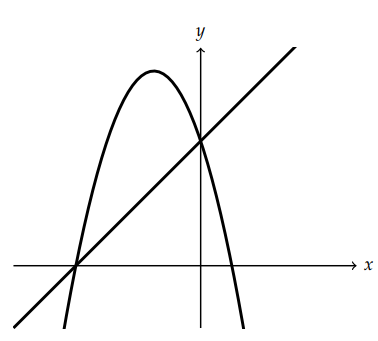
Assinale a opção cujas expressões podem ser representadas pelos gráficos.
(A) \( y = -x^2 + 3x + 3 \) e \( y = x + 3 \)
(B) \( y = -x^2 + 3x + 4 \) e \( y = x + 4 \)
(C) \( y = -x^2 – 3x + 2 \) e \( y = x + 2 \)
(D) \( y = -x^2 – 5x – 4 \) e \( y = x – 4 \)
(E) \( y = -x^2 – 3x + 4 \) e \( y = x + 4 \)
(B) \( y = -x^2 + 3x + 4 \) e \( y = x + 4 \)
(C) \( y = -x^2 – 3x + 2 \) e \( y = x + 2 \)
(D) \( y = -x^2 – 5x – 4 \) e \( y = x – 4 \)
(E) \( y = -x^2 – 3x + 4 \) e \( y = x + 4 \)
Resposta correta: (E)
1º Passo: A parábola é côncava para baixo (\(a < 0\)), então a função quadrática tem coeficiente \(a = -1\).
2º Passo: Pela figura, a reta corta o eixo \(y\) em \(y=4\), logo sua equação é \(y = x + 4\).
3º Passo: Observando que a parábola corta o eixo \(x\) em \((-4,0)\) e \((0,4)\), temos: \[ y = -x^2 – 3x + 4 \]
✅ Portanto, a alternativa correta é E.
🔗 Continue seus estudos: