Questão 6 – Altura de um Helicóptero

Questão 6

Enunciado: Considere duas pessoas a 4 km de distância uma da outra, localizadas em dois pontos \(A\) e \(B\) no solo. A pessoa no ponto \(A\), olhando na direção de \(B\), avistou, segundo um ângulo de \(50^\circ\) com a horizontal, um helicóptero. No mesmo instante, a pessoa no ponto \(B\), olhando na direção de \(A\), avistou o mesmo helicóptero segundo um ângulo de \(45^\circ\) com a horizontal. Aproximadamente, a que altura do solo o helicóptero estava naquele momento? Considere:

\(sen 45^\circ = \cos 45^\circ \quad \text{e} \quad tg 50^\circ \approx 1,19\)

Mostrar/Esconder Solução

Solução Passo a Passo:

Seja \(h\) a altura do helicóptero e \(x\) a distância do ponto \(A\) à projeção vertical do helicóptero no solo. Então:

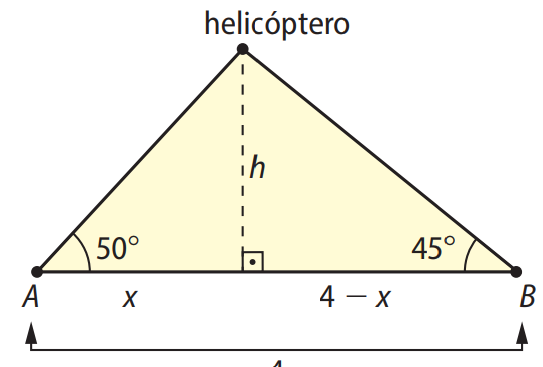
\(tg 45^\circ = \frac{h}{4 – x} \Rightarrow 1 = \frac{h}{4 – x} \Rightarrow h = 4 – x \Rightarrow x = 4 – h\)

Para o ponto \(A\), temos:

\(tg 50^\circ = \frac{h}{x} \Rightarrow 1,19 = \frac{h}{4 – h}\)

Resolvendo:

\(1,19 (4 – h) = h \Rightarrow 4,76 – 1,19h = h \Rightarrow 4,76 = 2,19h \Rightarrow h \approx 2,17 \, \text{km}\)

Resposta: A altura aproximada do helicóptero é 2,17 km ou 2.170 m.

---

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Explore Mais Conteúdos de Trigonometria

➡ Domine a Trigonometria no Triângulo Retângulo com Exemplos ➡ Razões Trigonométricas no Triângulo Retângulo

Relacionadas

Matemática para Concursos: Geometria Espacial – Banca VUNESP - Nível Superior

Matemática para Concursos: Geometria Espacial – Banca VUNESP - Nível Médio

Matemática para Concursos: Geometria Espacial – Banca VUNESP - Nível Superior