(CESPE / CEBRASPE 2021 – SEED-PR – Professor – Educação Básica e Jornada)
Um mesmo trabalho pode ser realizado por João e Pedro em 6 dias; por Pedro e José em 8 dias; ou por João e José em 12 dias.
Nesse caso, para fazer o trabalho sozinho, João levará
A) 32 dias.
B) 26 dias.
C) 20 dias.
D) 16 dias.
E) 14 dias.
Vamos resolver o problema utilizando o conceito de trabalho em conjunto. Para isso, consideraremos que João, Pedro e José têm produtividades diferentes ao realizar o trabalho.
Passo 1: Definindo as Produtividades
Vamos definir:
- ( J ) como a quantidade de trabalho que João faz em 1 dia.
- ( P ) como a quantidade de trabalho que Pedro faz em 1 dia.
- ( Z ) como a quantidade de trabalho que José faz em 1 dia.
Passo 2: Equações Baseadas nas Informações
Dado que:
João e Pedro juntos realizam o trabalho em 6 dias:
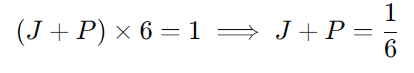
Pedro e José juntos realizam o trabalho em 8 dias:
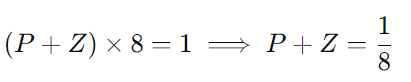
João e José juntos realizam o trabalho em 12 dias:
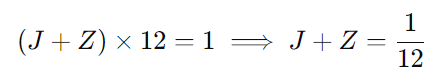
Passo 3: Sistema de Equações
Agora temos o seguinte sistema de equações:
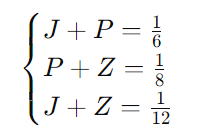
Vamos somar todas as três equações:
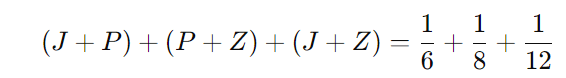
Simplificando:
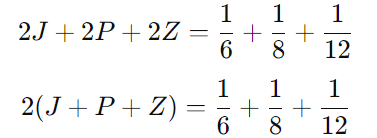
Agora vamos encontrar o MMC (Mínimo Múltiplo Comum) de 6, 8 e 12, que é 24:
Passo 4: Encontrando o Valor de J
Vamos agora encontrar o valor de ( J ):
Subtraindo a segunda equação da soma das três:
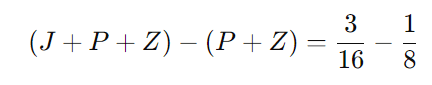
Convertendo as frações para o mesmo denominador (16):
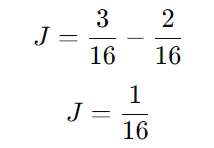
Passo 5: Calculando o Tempo de João
João realiza 1/16 do trabalho em 1 dia. Logo, ele levará:
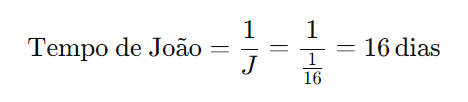
Resposta
João levará 16 dias para fazer o trabalho sozinho.
Alternativa correta: D) 16 dias.

























