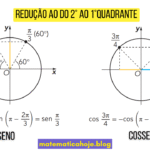
Redução ao 1º Quadrante: Ângulos do 4º Quadrante
O estudo da circunferência trigonométrica mostra que é possível reduzir ângulos maiores a ângulos de referência no 1º quadrante. Aqui veremos como funciona a redução de ângulos do 4º quadrante para o 1º quadrante, aplicando-se principalmente às funções seno e cosseno.
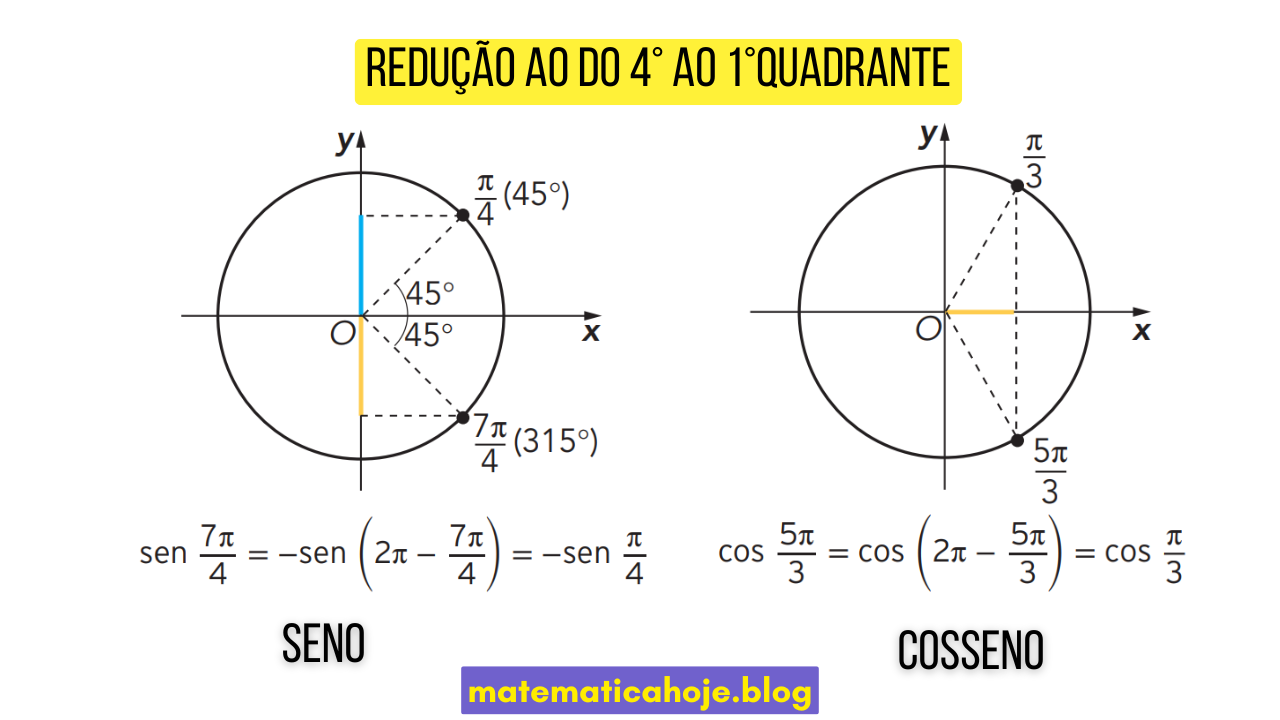
Ideia principal da redução (4º → 1º)
No 4º quadrante \(\left(\tfrac{3\pi}{2}<\theta<2\pi\right)\), os sinais são:
seno negativo e cosseno positivo.
- \(\displaystyle sen\theta=-sen(2\pi-\theta)\)
- \(\displaystyle \cos\theta=\cos(2\pi-\theta)\)
Assim, obtemos um ângulo no 1º quadrante, onde os valores trigonométricos são facilmente encontrados usando ângulos notáveis.
Exemplos resolvidos
1) \(\theta=\tfrac{7\pi}{4}=315^\circ\)
2) \(\theta=\tfrac{5\pi}{3}=300^\circ\)
Note que essa técnica reduz a qualquer ângulo equivalente no 1º quadrante.
Exercícios de múltipla escolha
1) O valor de \(sen(330^\circ)\) é:
- \(\tfrac{1}{2}\)
- \(-\tfrac{1}{2}\)
- \(\tfrac{\sqrt{3}}{2}\)
- \(-\tfrac{\sqrt{3}}{2}\)
Ver solução
\(330^\circ=360^\circ-30^\circ\Rightarrowsen(330^\circ)=-sen(30^\circ)=-\tfrac{1}{2}\). Alternativa B.
2) O valor de \(\cos(315^\circ)\) é:
- \(\tfrac{\sqrt{2}}{2}\)
- \(-\tfrac{\sqrt{2}}{2}\)
- \(\tfrac{1}{2}\)
- \(-\tfrac{1}{2}\)
Ver solução
\(315^\circ=360^\circ-45^\circ\Rightarrow\cos(315^\circ)=\cos(45^\circ)=\tfrac{\sqrt{2}}{2}\). Alternativa A.
Mais prática? Acesse o Banco de Questões para exercitar reduções trigonométricas.
Leia também (links internos)
📚 Produtos recomendados do blog
🧠 Mapas Mentais de Matemática
Visualize os sinais de seno e cosseno em cada quadrante.
Ver Mapas Mentais🎯 ENEM Matemática
Questões de trigonometria que exploram reduções de quadrante.
Acessar ENEM Matemática📘 10 eBooks de Matemática
Material completo com reduções, exemplos e exercícios resolvidos.
Baixar os 10 eBooks📝 Banco de Questões de Matemática
Milhares de exercícios prontos para praticar reduções trigonométricas.
Abrir Banco de Questões👨🏫 Canais Oficiais de Matemática
Receba materiais exclusivos e dicas de trigonometria diretamente no seu WhatsApp.
Entrar nos Canais