Relação de Pascal — O Que É, Fórmula, Interpretação e Exercícios Resolvidos

A Relação de Pascal é uma identidade clássica dos coeficientes binomiais (combinações) e aparece o tempo todo em Análise Combinatória. Ela conecta três combinações de forma simples e poderosa — e explica, na prática, por que o Triângulo de Pascal “se constrói somando dois números de cima”.

Se você domina esta relação, você ganha velocidade em questões de ENEM e concursos (simplificação de expressões, identidades e contas com combinações).

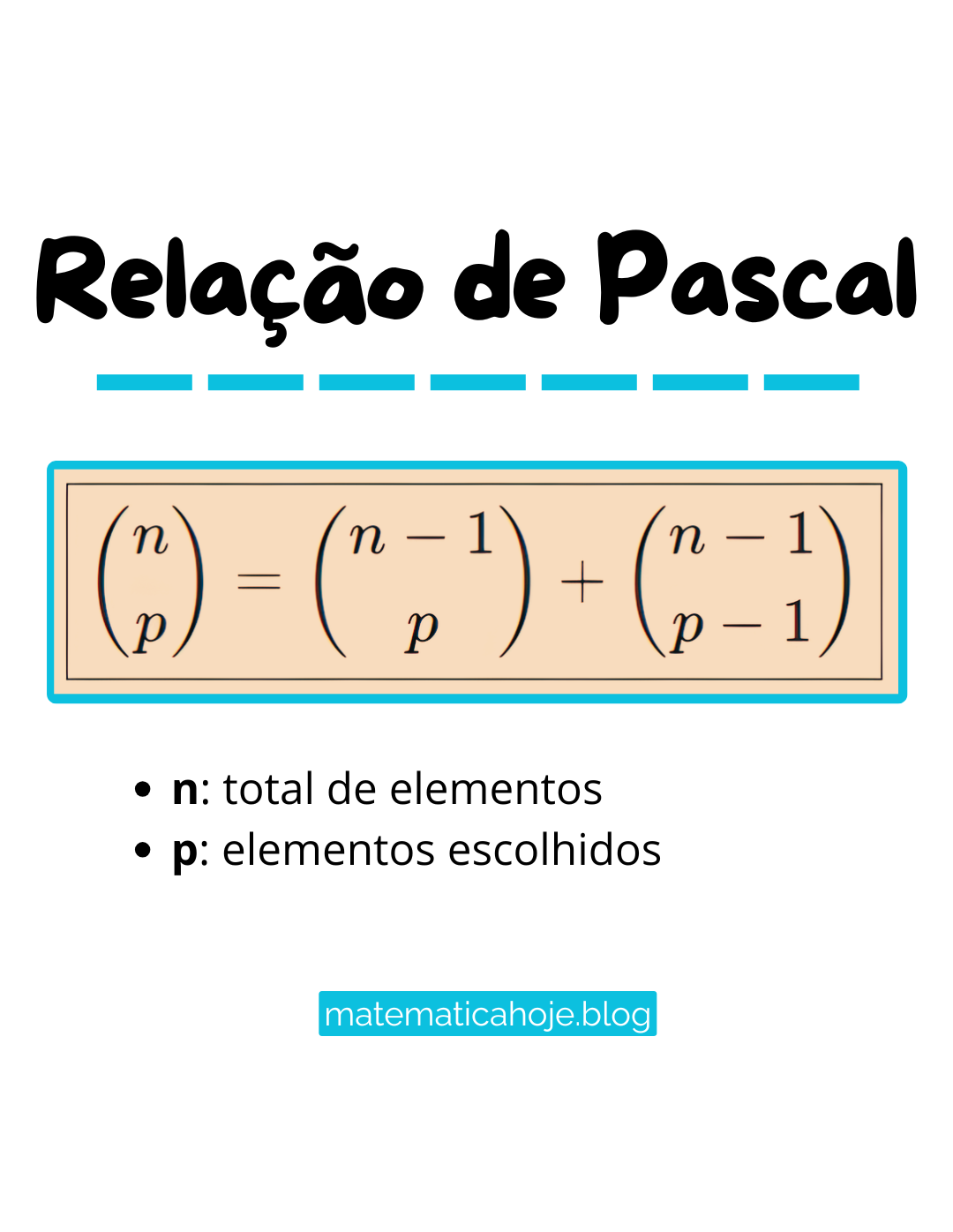
Relação de Pascal: (n p) = (n-1 p) + (n-1 p-1)

O que é a Relação de Pascal?

A relação afirma que:

\[ \binom{n}{p}=\binom{n-1}{p}+\binom{n-1}{p-1} \]

Onde cada símbolo tem um papel bem claro:

n: total de elementos do conjunto;
p: quantidade de elementos escolhidos;
\(\binom{n}{p}\): número de formas de escolher p elementos entre n (ordem não importa).

Leitura rápida:

“Escolher p entre n” é o mesmo que somar:

as escolhas de p entre n−1 (quando um elemento específico fica fora);
com as escolhas de p−1 entre n−1 (quando esse elemento específico entra).

Interpretação Intuitiva (a mais cobrada)

Imagine um conjunto com n elementos e escolha um elemento especial (por exemplo, o elemento “A”). Ao formar um grupo com p elementos:

Caso 1: o elemento “A” não entra → você escolhe \(p\) entre os \(n-1\) restantes → \(\binom{n-1}{p}\).
Caso 2: o elemento “A” entra → falta escolher \(p-1\) entre os \(n-1\) restantes → \(\binom{n-1}{p-1}\).

Como os casos não se misturam, somamos:

\[ \binom{n}{p}=\binom{n-1}{p}+\binom{n-1}{p-1} \]

Ligação direta com Combinação e Fatorial

A base de tudo é a combinação simples:

\[ \binom{n}{p}=\frac{n!}{p!(n-p)!} \]

Para manipulações algébricas, o fatorial quase sempre aparece (e ajuda a simplificar expressões com rapidez).

Relação de Pascal no Triângulo de Pascal

A ideia por trás do Triângulo de Pascal é exatamente esta: cada número interno do triângulo é a soma de dois acima. Em linguagem de binomiais, é a Relação de Pascal funcionando linha a linha.

Exemplos resolvidos

Exemplo 1

Use a Relação de Pascal para calcular \(\binom{6}{2}\).

Ver solução

Aplicando a relação:

\[ \binom{6}{2}=\binom{5}{2}+\binom{5}{1} \]

Agora calcule:

\[ \binom{5}{2}=10 \qquad \binom{5}{1}=5 \] \[ \binom{6}{2}=10+5=15 \]

Resposta: \(\boxed{15}\).

Exemplo 2

Mostre que \(\binom{8}{3}=\binom{7}{3}+\binom{7}{2}\).

Ver solução

Basta comparar com a fórmula:

\[ \binom{n}{p}=\binom{n-1}{p}+\binom{n-1}{p-1} \]

Aqui \(n=8\) e \(p=3\), então:

\[ \binom{8}{3}=\binom{7}{3}+\binom{7}{2} \]

Conclusão: identidade verdadeira.

Quando usar (em prova)?

Use a Relação de Pascal quando:

aparecer soma de combinações “parecidas”, do tipo \(\binom{n-1}{p}+\binom{n-1}{p-1}\);
você precisar reduzir uma conta grande para duas menores;
o enunciado mencionar Triângulo de Pascal ou “somar dois termos acima”.

Se você quiser revisar o caminho completo do tema, siga: PFC → Fatorial → Arranjo Simples → Permutação → Combinação.