Relações Métricas no Triângulo Retângulo

O estudo das relações métricas em um triângulo retângulo é fundamental para resolver problemas de geometria, trigonometria e até de física. Essas relações envolvem os lados do triângulo, sua altura relativa à hipotenusa e os segmentos que essa altura determina.

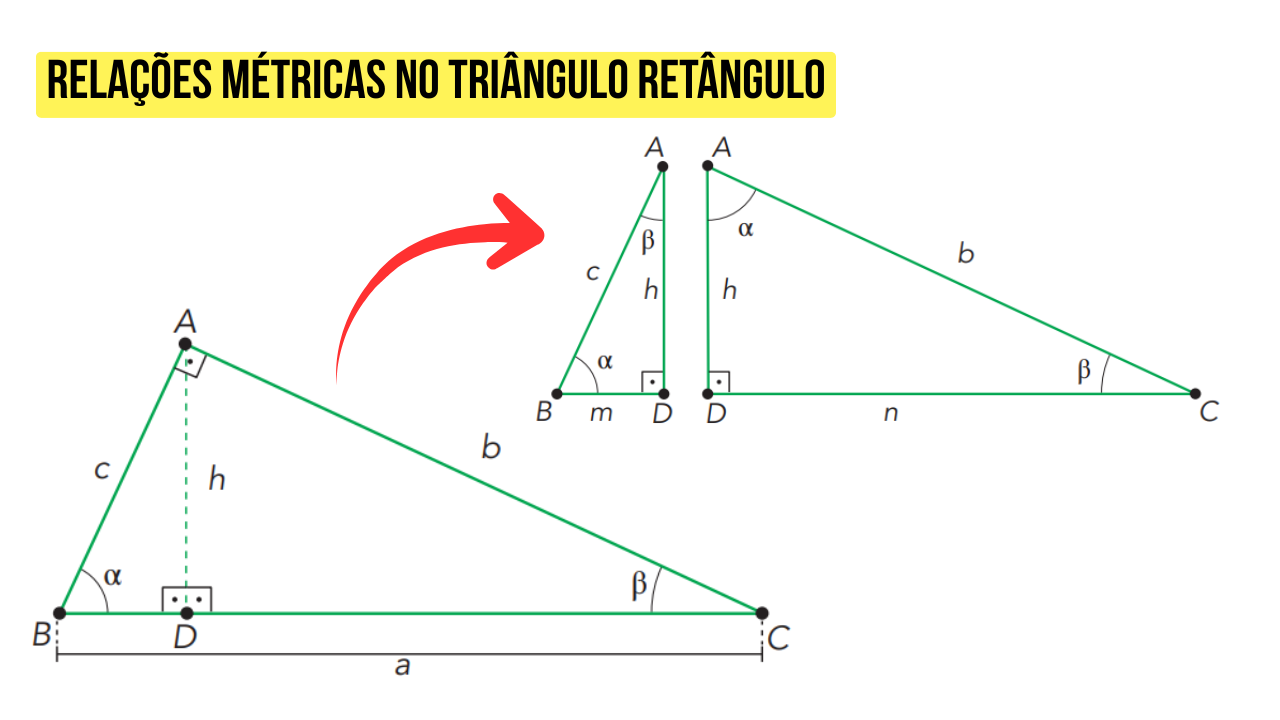
Principais Relações Métricas

Seja um triângulo retângulo \(ABC\), com hipotenusa \(a\), catetos \(b\) e \(c\), altura relativa à hipotenusa \(h\) e projeções \(m\) e \(n\), temos:

1. \( h^2 = m \cdot n \) (quadrado da altura = produto das projeções)

2. \( b^2 = a \cdot m \) (quadrado de um cateto = hipotenusa × projeção do cateto)

3. \( c^2 = a \cdot n \)

4. \( a \cdot h = b \cdot c \) (produto da hipotenusa pela altura = produto dos catetos)

Exemplo Resolvido

Exemplo: Em um triângulo retângulo, a hipotenusa mede 10 cm e uma projeção mede 6 cm. Calcule a altura relativa à hipotenusa.

Pela relação: \( h^2 = m \cdot n \).

Sabemos que \( a = 10 \), \( m = 6 \). Logo, \( n = a – m = 10 – 6 = 4 \).

\( h^2 = 6 \cdot 4 = 24 \Rightarrow h = \sqrt{24} \approx 4,9 \, cm \).

📘 Exercícios de Múltipla Escolha

1) Em um triângulo retângulo, a hipotenusa mede 13 cm e um cateto mede 12 cm. A projeção desse cateto sobre a hipotenusa é:

9 cm
11,08 cm
12 cm
10 cm

Ver solução

Relação: \( b^2 = a \cdot m \). Logo, \( 12^2 = 13 \cdot m \Rightarrow m = \frac{144}{13} \approx 11,08 \, cm \).

2) Em um triângulo retângulo, os catetos medem 6 cm e 8 cm. A altura relativa à hipotenusa vale:

4 cm
4,8 cm
5 cm
6 cm

Ver solução

\( h = \frac{b \cdot c}{a} \). Como \( a = 10 \), temos \( h = \frac{6 \cdot 8}{10} = 4,8 \, cm \).

3) A altura relativa à hipotenusa mede 12 cm, e as projeções dos catetos sobre a hipotenusa valem \(m\) e \(n\). Sabendo que \(m=9\), determine \(n\).