O triângulo retângulo é uma das figuras geométricas mais estudadas na matemática, especialmente por causa de suas propriedades e relações métricas. Estas relações permitem calcular com precisão diversas medidas no triângulo, como comprimentos dos lados, projeções e altura, com base em poucos dados. Neste artigo, exploraremos as principais relações métricas que envolvem a hipotenusa, os catetos, as projeções e a altura em um triângulo retângulo.
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
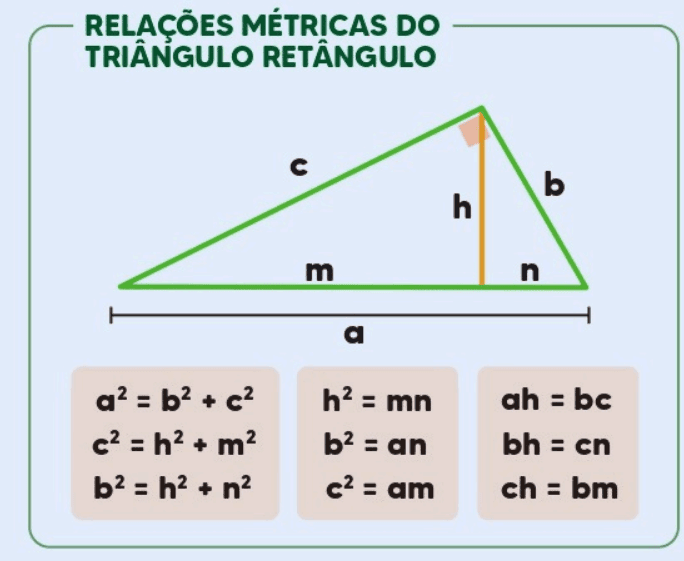
Elementos de um Triângulo Retângulo
Antes de discutirmos as fórmulas, é importante definir os elementos principais de um triângulo retângulo:
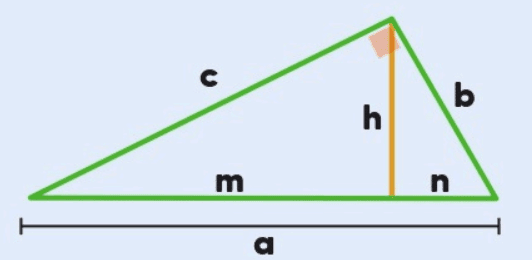
- Hipotenusa (a): O lado oposto ao ângulo reto.
- Catetos (b e c): Os dois lados que formam o ângulo reto.
- Projeção de b sobre a hipotenusa (n): O segmento da hipotenusa que é “projetado” pelo cateto b.
- Projeção de c sobre a hipotenusa (m): O segmento da hipotenusa que é “projetado” pelo cateto c.
- Altura (h): O segmento que parte do vértice do ângulo reto e é perpendicular à hipotenusa.
Relações Métricas Fundamentais
Aqui estão as principais relações métricas em um triângulo retângulo, utilizando as notações mencionadas:
- Teorema de Pitágoras:
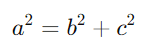
Esta é a relação mais conhecida, que afirma que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Relação do Cateto com a Projeção: Para os catetos b e c, temos:
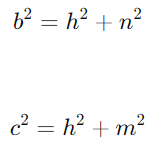
Estas fórmulas expressam que o quadrado de cada cateto é igual à soma dos quadrados da altura e da respectiva projeção na hipotenusa.
Relação da Altura com as Projeções:
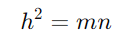
A altura ao quadrado é igual ao produto das projeções dos catetos sobre a hipotenusa.
Relações entre Catetos e Projeções na Hipotenusa:
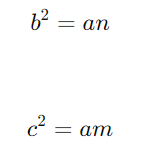
Aqui, o quadrado de um cateto é igual ao produto da hipotenusa pela projeção do outro cateto.
Relação Entre a Hipotenusa, Altura e Catetos:
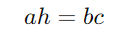
O produto da hipotenusa pela altura é igual ao produto dos catetos.
Relações de Projeção:
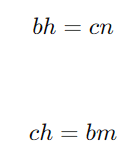
Estas expressões mostram que o produto de um cateto pela altura é igual ao produto da projeção do outro cateto pela hipotenusa.
Aplicações Práticas das Relações Métricas
As relações métricas no triângulo retângulo têm uma vasta gama de aplicações práticas. Elas são utilizadas em problemas de engenharia, arquitetura, navegação e diversas outras áreas. Aqui estão algumas aplicações:
1. Cálculo de Alturas e Distâncias
Em situações onde é necessário determinar a altura de uma estrutura, como uma torre ou um edifício, essas relações permitem calcular a altura a partir de medidas tomadas ao nível do solo.
2. Construção Civil
Na construção, as relações métricas ajudam a garantir que as estruturas sejam construídas de forma precisa e segura. Por exemplo, ao verificar a inclinação de rampas ou escadas, as fórmulas são fundamentais para garantir que a inclinação esteja dentro dos padrões desejados.
3. Desenho Técnico
Engenheiros e arquitetos utilizam essas relações para projetar e desenhar plantas e modelos, garantindo que as proporções e ângulos sejam precisos.
Conclusão
As relações métricas no triângulo retângulo são ferramentas poderosas para resolver problemas geométricos e práticos. Com base em simples medidas de lados e projeções, é possível calcular com precisão diversas outras grandezas, facilitando a análise e construção de projetos em diversas áreas. O entendimento e aplicação dessas relações é essencial para qualquer estudante ou profissional que lide com geometria e suas aplicações.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes




























