Reta Perpendiculares

Retas Perpendiculares — Definição, Fórmulas e Exemplos

Retas Perpendiculares — Definição, Fórmula e Exemplos

As retas perpendiculares são um conceito essencial da Geometria Analítica. Elas representam duas retas que se cruzam formando um ângulo reto (90°). Essa relação é expressa por uma condição simples entre seus coeficientes angulares.

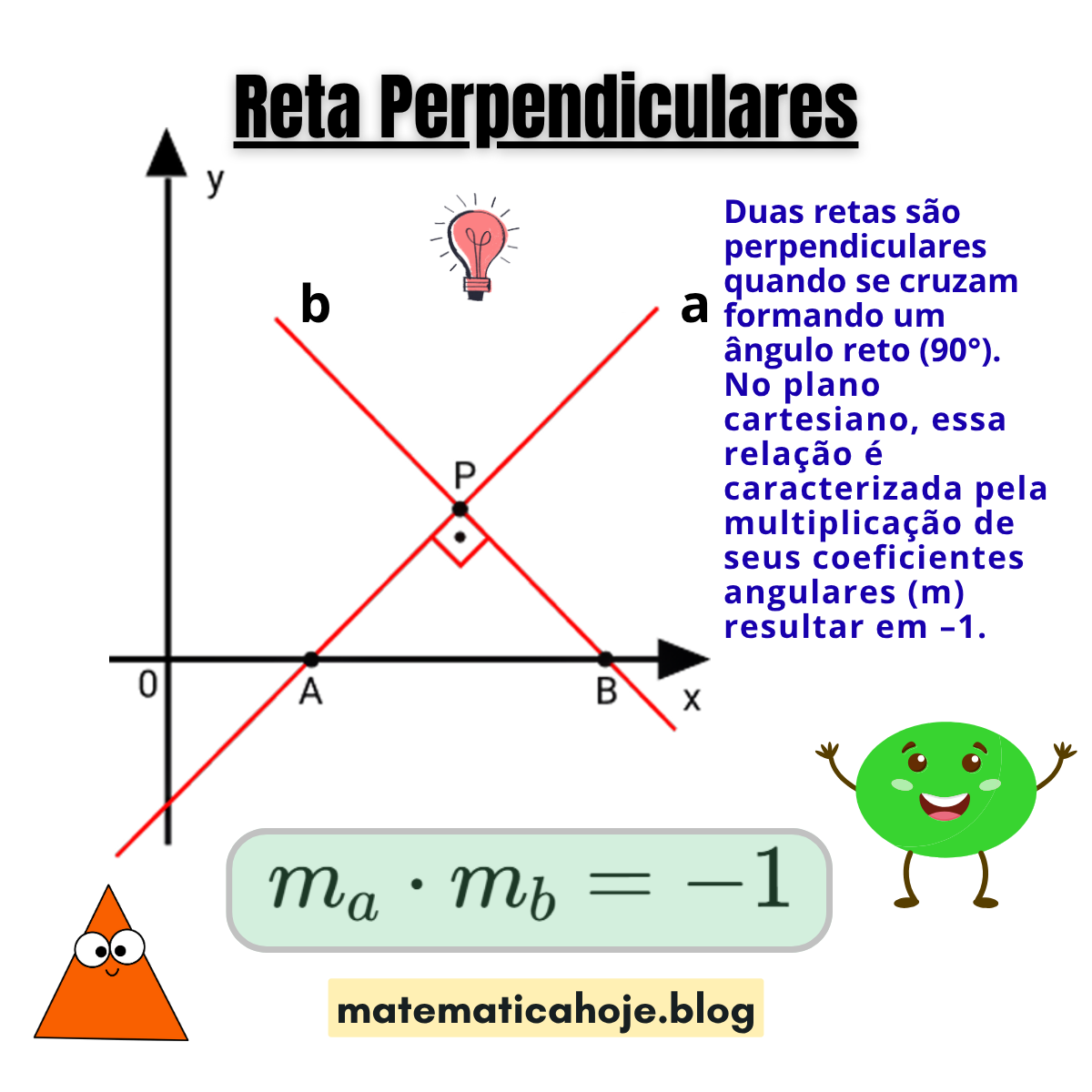
Retas perpendiculares no plano cartesiano - matematicaoje.blog

📘 O que são Retas Perpendiculares

No plano cartesiano, dizemos que duas retas \( a \) e \( b \) são perpendiculares quando se encontram formando um ângulo de 90°, ou seja, são linhas que se cruzam de maneira perfeitamente “reta”.

Matematicamente, essa relação é caracterizada pela multiplicação de seus coeficientes angulares resultar em –1:

\( m_a \cdot m_b = -1 \)

Isso significa que o coeficiente angular de uma reta é o inverso negativo do coeficiente angular da outra.

💡 Se uma reta tem inclinação \( m = 2 \), então a reta perpendicular a ela terá \( m = -\frac{1}{2} \).

🧩 Entendendo o Coeficiente Angular

O coeficiente angular \( m \) indica a inclinação da reta em relação ao eixo \(x\). Quando duas retas são perpendiculares, a multiplicação de suas inclinações gera um resultado negativo, mostrando que uma se inclina em direção oposta à outra, formando 90°.

📐 Exemplo 1

Exemplo: A reta \( r \) tem coeficiente angular \( m_r = 3 \). Determine o coeficiente angular da reta \( s \), perpendicular a \( r \).

Pela condição de perpendicularidade: \( m_r \cdot m_s = -1 \) Substituindo \( m_r = 3 \): \( 3 \cdot m_s = -1 \Rightarrow m_s = -\frac{1}{3} \) ✅ Assim, o coeficiente angular da reta perpendicular é \( m_s = -\frac{1}{3} \).

📐 Exemplo 2

Exemplo: Verifique se as retas \( y = 2x + 1 \) e \( y = -\frac{1}{2}x + 3 \) são perpendiculares.

O coeficiente angular da primeira é \( m_1 = 2 \) e da segunda é \( m_2 = -\frac{1}{2} \). Verificando: \( m_1 \cdot m_2 = 2 \times (-\frac{1}{2}) = -1 \) ✅ Logo, as retas são **perpendiculares**.

📘 Domine TODAS as Fórmulas de Matemática!

Baixe o eBook Fórmulas Matemática e tenha acesso às principais fórmulas de Geometria, Álgebra e Trigonometria — organizadas de forma clara e prática para seus estudos e revisões.

📥 Baixar Agora — É Grátis!

📚 Exercícios de Fixação

1. A reta \( r: y = 4x + 2 \) é perpendicular à reta \( s: y = -\frac{1}{4}x – 1 \)?

\( m_r = 4 \) e \( m_s = -\frac{1}{4} \). \( m_r \cdot m_s = 4 \times (-\frac{1}{4}) = -1 \) ✅ São **perpendiculares**.

2. Determine o coeficiente angular da reta perpendicular à reta \( y = -3x + 2 \).

\( m_1 = -3 \Rightarrow m_2 = -\frac{1}{m_1} = \frac{1}{3} \). ✅ O coeficiente angular da reta perpendicular é \( \frac{1}{3} \).

🔗 Continue Estudando

Relacionadas

Coeficiente Linear

Distância entre Dois Pontos

Divisão de um Segmento em uma Razão Dada

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.