No estudo da geometria, entender as relações entre retas paralelas e transversais é fundamental para resolver muitos problemas e provar teoremas. Neste artigo, exploraremos os principais conceitos relacionados a retas paralelas e transversais, incluindo os ângulos opostos pelo vértice, ângulos correspondentes, ângulos alternos internos e ângulos alternos externos.
1. Retas Paralelas e Transversais
Definição:
- Retas Paralelas: Duas retas são paralelas se nunca se encontram, não importa o quanto sejam estendidas. Elas estão na mesma direção e permanecem a uma distância constante uma da outra.
- Transversal: Uma transversal é uma linha que cruza duas ou mais retas paralelas em diferentes pontos. Essa interseção cria vários pares de ângulos que têm propriedades específicas.
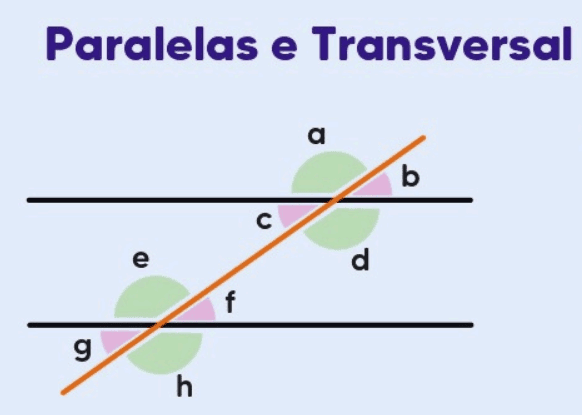
2. Ângulos Opostos pelo Vértice (OPV)
Definição:
- Ângulos Opostos pelo Vértice: Quando duas retas se cruzam, os ângulos formados em cada lado da interseção são chamados de ângulos opostos pelo vértice. Esses ângulos são iguais em medida.
Características:
- Ângulos opostos pelo vértice são sempre congruentes.
- Se as retas são paralelas e a transversal cruza-as, os ângulos opostos pelo vértice formados são também iguais.

Exemplo: Quando duas retas paralelas são cortadas por uma transversal, os ângulos formados no mesmo lado da transversal e no mesmo ponto de interseção são opostos pelo vértice e são iguais.
3. Ângulos Correspondentes
Definição:
- Ângulos Correspondentes: Quando uma transversal corta duas retas paralelas, ela forma ângulos correspondentes em cada lado da transversal, na mesma posição relativa em relação à reta paralela.
Características:
- Ângulos correspondentes são sempre iguais se as retas forem paralelas.
- Eles estão localizados em posições correspondentes, por exemplo, um ângulo no canto superior direito de uma interseção e o ângulo no canto superior direito da outra interseção.
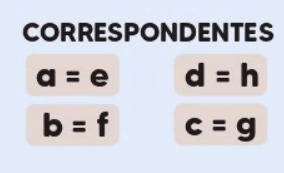
Exemplo: Se uma transversal corta duas retas paralelas, o ângulo formado no canto superior esquerdo da interseção de uma reta com a transversal é igual ao ângulo no canto superior esquerdo da interseção da outra reta com a transversal.
4. Ângulos Alternos Internos
Definição:
- Ângulos Alternos Internos: São os ângulos que estão em lados opostos da transversal e dentro das duas retas paralelas.
Características:
- Ângulos alternos internos são congruentes quando as retas cortadas pela transversal são paralelas.
- Eles estão localizados em posições “alternadas” dentro das retas paralelas, um de cada lado da transversal.

Exemplo: Se uma transversal corta duas retas paralelas, o ângulo à esquerda da transversal e abaixo da linha paralela é igual ao ângulo à direita da transversal e abaixo da outra linha paralela.
5. Ângulos Alternos Externos
Definição:
- Ângulos Alternos Externos: São os ângulos que estão em lados opostos da transversal e fora das duas retas paralelas.
Características:
- Ângulos alternos externos são congruentes quando as retas cortadas pela transversal são paralelas.
- Eles estão localizados em posições “alternadas” fora das retas paralelas, um de cada lado da transversal.

Exemplo: Se uma transversal corta duas retas paralelas, o ângulo externo à esquerda da transversal e fora da linha paralela é igual ao ângulo externo à direita da transversal e fora da outra linha paralela.
Conclusão
Os conceitos de ângulos opostos pelo vértice, ângulos correspondentes, ângulos alternos internos e ângulos alternos externos são essenciais para a compreensão da geometria das retas paralelas e transversais. Conhecer essas propriedades ajuda na resolução de problemas matemáticos, na prova de teoremas e na aplicação prática em diversas áreas, como arquitetura e engenharia. Entender como esses ângulos se relacionam permite uma análise mais profunda das figuras geométricas e das suas propriedades.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes













