Sistemas lineares, matrizes e determinantes

Neste guia você verá como escrever um sistema na forma \(A\,\mathbf{x}=\mathbf{b}\) e como os determinantes ajudam a resolver e classificar sistemas \(2\times2\) e \(3\times3\) (SPD, SI, SPI). Também conectamos com matriz aumentada \([A\mid\mathbf{b}]\), posto (rank) e o teorema de Rouché–Capelli. Para aprofundar, veja: representação matricial, matrizes associadas, escalonamento (Gauss) e classificação.

📘 eBook Fórmulas Matemática — Cramer, Sarrus, Gauss e classificação

Todas as fórmulas de \(2\times2\) e \(3\times3\), passo a passo de Gauss/Gauss–Jordan, Regra de Cramer, determinantes e Rouché–Capelli. Perfeito para revisão antes da prova.

Quero o eBook Praticar no Banco de Questões

De \(A\mathbf{x}=\mathbf{b}\) aos determinantes

Para um sistema quadrado \(n\times n\):

\(\det(A)\neq0\Rightarrow\) \(A\) é invertível; o sistema é SPD e \(\mathbf{x}=A^{-1}\mathbf{b}=\dfrac{\operatorname{adj}(A)}{\det(A)}\,\mathbf{b}\) (Regra de Cramer).
\(\det(A)=0\Rightarrow\) não há inversa; o sistema pode ser SI ou SPI. Decida com o posto: se \(r(A)\neq r([A\mid\mathbf{b}])\) ⇒ SI; se \(r(A)=r([A\mid\mathbf{b}])

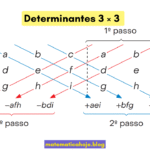
Como calcular determinantes

2×2: \(\det\!\begin{bmatrix}a&b\\c&d\end{bmatrix}=ad-bc\).
3×3 (Sarrus): replique as duas primeiras colunas e faça a soma das diagonais principais menos a das secundárias.

Exemplos resolvidos

1) Sistema 2×2 — Cramer direto

\(\begin{cases}5x+4y=1\\3x+7y=2\end{cases}\Rightarrow A=\begin{bmatrix}5&4\\3&7\end{bmatrix},\ \Delta=\det(A)=23\neq0\).

Conta

\(x=\dfrac{\det\!\begin{bmatrix}1&4\\2&7\end{bmatrix}}{23}=-\tfrac{1}{23}\),\quad \(y=\dfrac{\det\!\begin{bmatrix}5&1\\3&2\end{bmatrix}}{23}=\tfrac{7}{23}\). Logo \(S=\{(-\tfrac{1}{23},\tfrac{7}{23})\}\).

2) Sistema 3×3 — Sarrus + eliminação curta

\(\begin{cases} x+y+z=6\\ 2x-y+z=7\\ -x+2y-z=-1 \end{cases}\Rightarrow A=\begin{bmatrix}1&1&1\\2&-1&1\\-1&2&-1\end{bmatrix}\).

Classificação e solução

\(\det(A)=3\neq0\Rightarrow\) SPD. Eliminando: (2)−(1) ⇒ \(x-2y=1\); (3)+(1) ⇒ \(3y=5\Rightarrow y=\tfrac{5}{3}\); então \(x=1+2y=\tfrac{13}{3}\) e \(z=0\). Solução: \(\big(\tfrac{13}{3},\tfrac{5}{3},0\big)\).

3) Determinante zero: SI × SPI

\(\begin{cases}x+y=2\\2x+2y=4\end{cases}\) ⇒ \(r=r_a=1<2\) ⇒ SPI (por exemplo, \(x=2-y\)).
\(\begin{cases}x+y=2\\2x+2y=5\end{cases}\) ⇒ \(rSI.

Exercícios (com gabarito)

1) Escreva \(A\), \(\mathbf{x}\), \(\mathbf{b}\) e resolva: \(\{\,2x-3y=4,\ x+5y=1\,\}\).

Gabarito

\(A=\begin{bmatrix}2&-3\\1&5\end{bmatrix}\), \(\Delta=13\neq0\). \(y=-\dfrac{2}{13}\), \(x=\dfrac{23}{13}\).

2) Classifique \(\{\,x+y-2z=0,\ x-2y+z=3,\ 2x-y-z=-4\,\}\) usando \([A\mid\mathbf{b}]\).

Gabarito

Escalonando, surge \([0,0,0\mid-7]\) ⇒ \(r(A)=2\), \(r_a=3\) ⇒ SI.

3) \(\{\,2x+y+2z=9,\ x-y+z=2,\ 3x+2y+z=10\,\}\) (3×3). Resolva.

Gabarito

\((x,y,z)=\big(\tfrac{3}{2},\tfrac{5}{3},\tfrac{13}{6}\big)\).

4) Sistema com parâmetro: \(\{\,2x+3y=5,\ 4x+6y=10+m\,\}\). Classifique em função de \(m\).

Gabarito

2ª é o dobro da 1ª no LHS. Se \(m=0\) ⇒ SPI; se \(m\neq0\) ⇒ SI.

Conclusão

Determinantes são a ponte entre álgebra matricial e resolução de sistemas: se \(\det(A)\neq0\), use Cramer (ou \(A^{-1}\)); se \(\det(A)=0\), decida com o posto de \(A\) e de \([A\mid\mathbf{b}]\). Domine a montagem de \(A\,\mathbf{x}=\mathbf{b}\), pratique Sarrus/adição/Gauss e você classifica e resolve problemas com rapidez.

Para ter tudo à mão, use o eBook Fórmulas Matemática e treine no Banco de Questões.