Sólidos de Platão – tudo o que você precisa saber
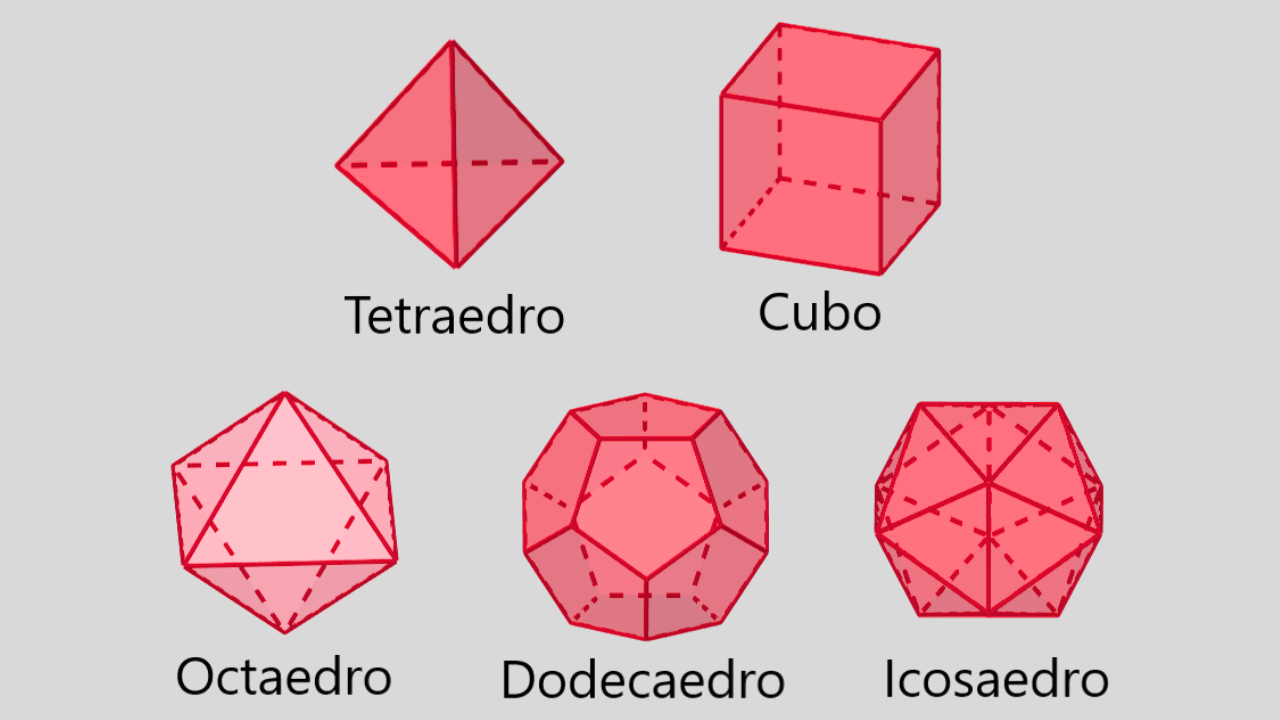
Há exatamente cinco poliedros convexos regulares: tetraedro, cubo, octaedro, dodecaedro e icosaedro. Em cada um deles, todas as faces são polígonos regulares congruentes e o mesmo número de faces se encontra em cada vértice. Este artigo traz definição, propriedades, fórmulas e uma prova curta de por que só existem cinco.
- a — comprimento da aresta (lado das faces);
- F — número de faces; V — número de vértices; A — número de arestas;
- A_t — área total; V\(_{\text{ol}}\) — volume.
Propriedades gerais
- São poliedros convexos regulares: faces congruentes, polígonos regulares; mesma quantidade de faces em cada vértice.
- Valem as fórmulas clássicas: Característica de Euler \(V-A+F=2\) e dupla regularidade (ângulos e arestas equivalentes por simetria).
- Relações de dualidade: tetraedro é autodual; cubo ↔ octaedro; dodecaedro ↔ icosaedro.
Tabelas (contagens e fórmulas)
Fórmulas em função da aresta \(a\). Áreas em unidades² e volumes em unidades³.
Triangulares e quadrado
| Sólido | Faces | Vértices | Arestas | Área \(A_t\) | Volume \(V\) |
|---|---|---|---|---|---|
| Tetraedro | 4 triâng. eq. | 4 | 6 | \( \sqrt{3}\,a^2 \) | \( \dfrac{a^3}{6\sqrt{2}} \) |
| Cubo (Hexaedro) | 6 quadrados | 8 | 12 | \( 6a^2 \) | \( a^3 \) |
| Octaedro | 8 triâng. eq. | 6 | 12 | \( 2\sqrt{3}\,a^2 \) | \( \dfrac{\sqrt{2}}{3}\,a^3 \) |
Pentágonos e triângulos
| Sólido | Faces | Vértices | Arestas | Área \(A_t\) | Volume \(V\) |
|---|---|---|---|---|---|
| Dodecaedro | 12 pentág. reg. | 20 | 30 | \( 3\sqrt{25+10\sqrt{5}}\;a^2 \) | \( \dfrac{15+7\sqrt{5}}{4}\;a^3 \) |
| Icosaedro | 20 triâng. eq. | 12 | 30 | \( 5\sqrt{3}\,a^2 \) | \( \dfrac{5}{12}\,(3+\sqrt{5})\,a^3 \) |
Tetraedro: \(4-6+4=2\); Cubo: \(8-12+6=2\); Octaedro: \(6-12+8=2\); Dodecaedro: \(20-30+12=2\); Icosaedro: \(12-30+20=2\).
Por que existem apenas cinco?
Seja \(p\) o número de lados de cada face e \(q\) o número de faces por vértice. O ângulo interno de um polígono regular de \(p\) lados é \( \alpha=180^\circ\!\left(1-\frac{2}{p}\right) \). Em um vértice, \(q\alpha<360^\circ\Rightarrow q\!\left(1-\frac{2}{p}\right)<2 \Rightarrow (p-2)(q-2)<4\).
As únicas soluções inteiras com \(p,q\ge3\) são: \((3,3)\) tetraedro; \((4,3)\) cubo; \((3,4)\) octaedro; \((5,3)\) dodecaedro; \((3,5)\) icosaedro. Logo, existem apenas cinco.
Dualidade e esferas
- Dualidade: trocar faces por vértices: cubo ↔ octaedro, dodecaedro ↔ icosaedro, tetraedro ↔ tetraedro.
- Todos possuem esfera inscrita (tangente às faces) e circunscrita (pelos vértices). Ex.: no cubo, \(r=a/2\) e \(R=\frac{\sqrt{3}}{2}a\).
Aplicações e conexões
- Modelagem 3D, estruturas moleculares (vírus icosaédricos), arte e arquitetura.
- Conexões com poliedros piramidais: pirâmides, pirâmide regular, triangular, quadrangular, hexagonal e cortes em tronco de pirâmide (razões de semelhança).
Exercícios rápidos (com gabarito)
\(A_t=\sqrt{3}a^2=36\sqrt{3}\ \text{cm}^2\). \(V=\dfrac{a^3}{6\sqrt{2}}=\dfrac{216}{6\sqrt{2}}=18\sqrt{2}\ \text{cm}^3\).
\(6a^2=150 \Rightarrow a=5\ \text{cm}\). Volume \(=a^3=125\ \text{cm}^3\).
\(a^3=\dfrac{150}{\sqrt{2}}\approx106{,}07\Rightarrow a\approx4{,}74\ \text{cm}\).
\(A_t=12\sqrt{25+10\sqrt{5}}\ \text{cm}^2\approx 247{,}74\ \text{cm}^2\).
No icosaedro, \(F=20\), \(A=30\), \(V=12\). Então \(V-A+F=12-30+20=2\). ✔️













