Teorema das Projeções — Guia Completo
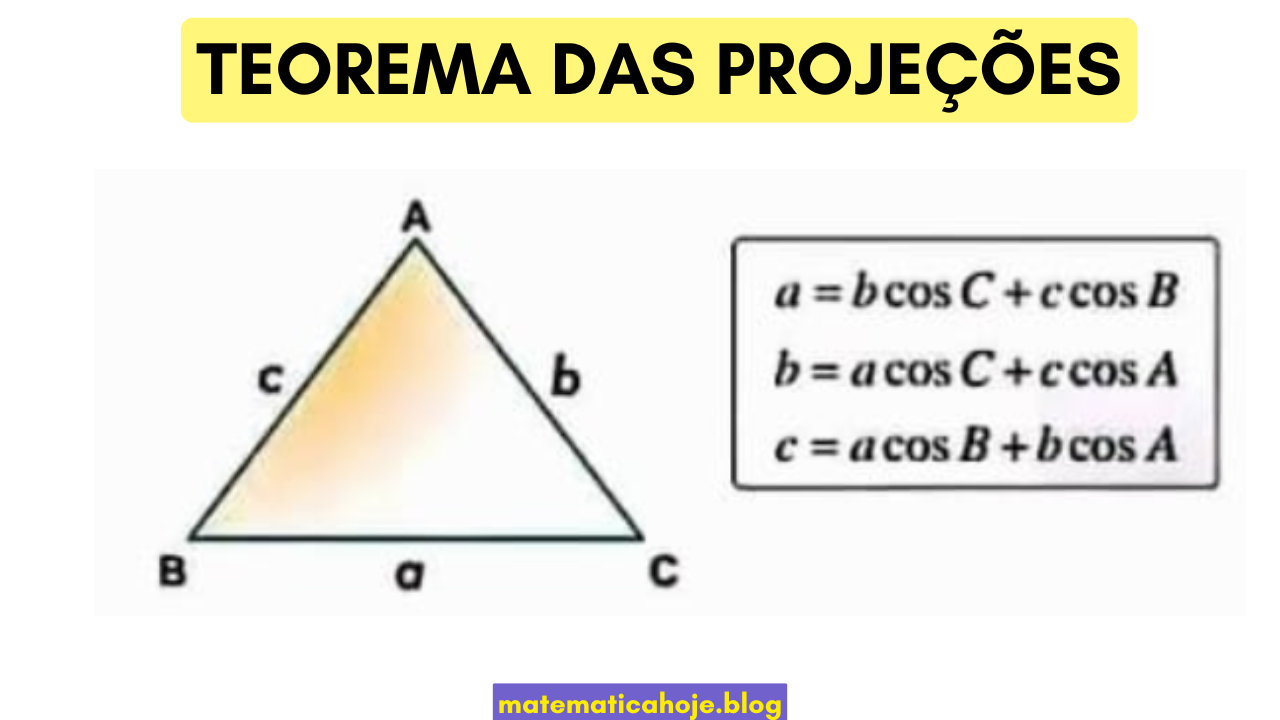
O Teorema das Projeções é um resultado importante da geometria e da trigonometria dos triângulos. Ele estabelece uma relação entre os lados de um triângulo e as projeções desses lados sobre a base de outros ângulos. Essencialmente, ele expressa um lado como a soma de projeções dos outros dois.
Enunciado
Num triângulo \(ABC\), com lados \(a, b, c\) opostos, respectivamente, aos ângulos \(A, B, C\), o Teorema das Projeções afirma:
Demonstração (esboço)
Considere o triângulo \(ABC\). Para provar a relação de \(a\), podemos projetar os lados \(b\) e \(c\) sobre o lado \(a\).
- A projeção de \(b\) sobre \(a\) é \(b \cos C\).
- A projeção de \(c\) sobre \(a\) é \(c \cos B\).
Somando essas projeções, temos:
\[ a = b \cos C + c \cos B \]De forma análoga, obtemos as outras duas fórmulas trocando as posições de \(a, b, c\) e seus ângulos correspondentes.
Aplicações
- Encontrar comprimentos de lados quando ângulos e projeções são conhecidos.
- Resolver triângulos sem precisar recorrer sempre à Lei dos Cossenos.
- Provar relações em problemas de geometria de concursos e olimpíadas.
Exemplos resolvidos
Exemplo 1
No triângulo \(ABC\), temos \(b=8\), \(c=6\), \(B=60^\circ\) e \(C=45^\circ\). Calcule \(a\).
Ver solução
Resposta: \(a \approx 11,66\)
Exemplo 2
Num triângulo, \(a=10\), \(c=7\), \(A=60^\circ\) e \(C=45^\circ\). Determine \(b\).
Ver solução
Resposta: \(b \approx 10,57\)
Exercícios sugeridos
1) Em \(ABC\), \(b=12\), \(c=9\), \(B=60^\circ\) e \(C=30^\circ\). Calcule \(a\).
\(a = b \cos C + c \cos B\).
Solução esperada: \(a \approx 15,79\).
2) Num triângulo, \(a=14\), \(c=10\), \(A=45^\circ\) e \(C=60^\circ\). Encontre \(b\).
\(b = a \cos C + c \cos A\).
Solução esperada: \(b \approx 12,90\).
Conclusão
O Teorema das Projeções é uma ferramenta poderosa para decompor lados de um triângulo em função de projeções. Ele serve como uma alternativa prática à Lei dos Cossenos em certos problemas e ajuda a entender melhor a estrutura geométrica de um triângulo.






















