Teorema de Tangentes (Lei das Tangentes): guia completo com demonstração, exemplos e exercícios

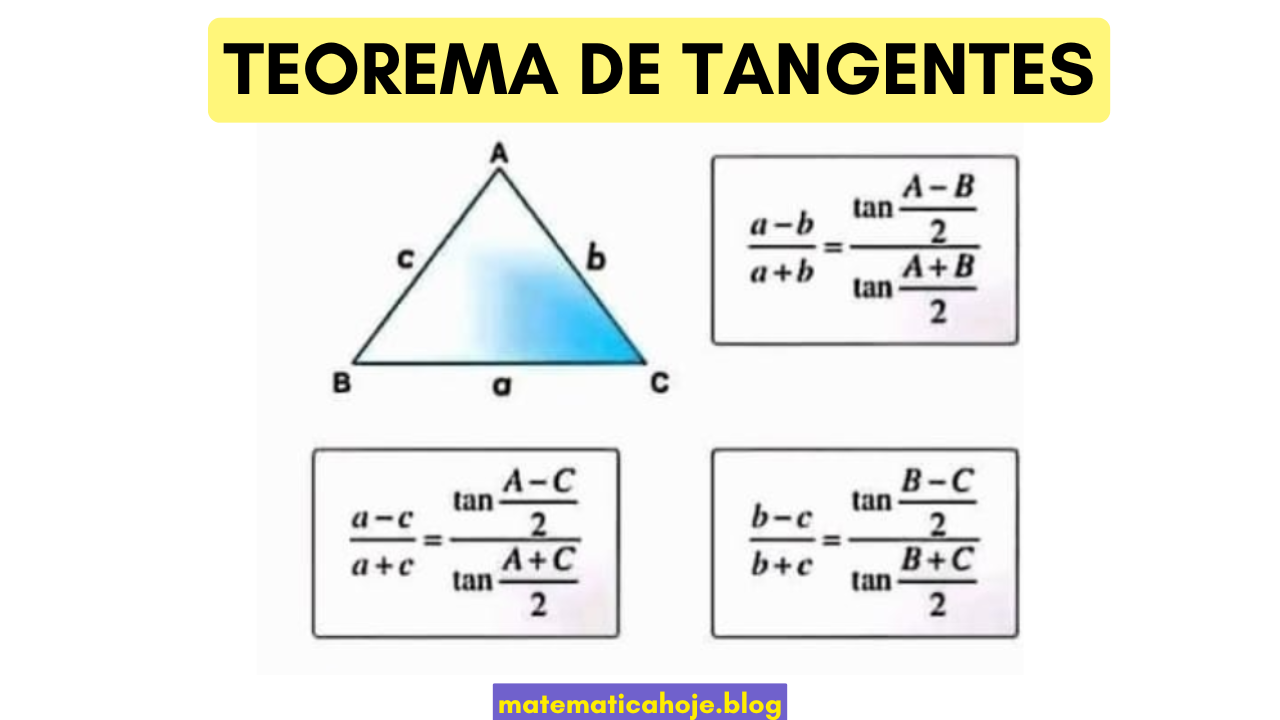
A Lei das Tangentes relaciona as diferenças e somass de lados de um triângulo com as tangentes das meias diferenças e meias somas dos ângulos correspondentes. É uma ferramenta elegante que complementa a Lei dos Senos e a Lei dos Cossenos, especialmente útil quando aparecem diferenças de lados/ângulos.

Enunciado e fórmulas

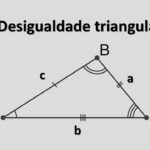
No triângulo \(ABC\), com lados \(a,b,c\) opostos, respectivamente, aos ângulos \(A,B,C\), valem as identidades:

Forma 1 (entre \(a\) e \(b\))

\[ \frac{a-b}{a+b} \;=\; \frac{\tan\!\left(\dfrac{A-B}{2}\right)}{\tan\!\left(\dfrac{A+B}{2}\right)} \]

Forma 2 (entre \(a\) e \(c\))

\[ \frac{a-c}{a+c} \;=\; \frac{\tan\!\left(\dfrac{A-C}{2}\right)}{\tan\!\left(\dfrac{A+C}{2}\right)} \]

Forma 3 (entre \(b\) e \(c\))

\[ \frac{b-c}{b+c} \;=\; \frac{\tan\!\left(\dfrac{B-C}{2}\right)}{\tan\!\left(\dfrac{B+C}{2}\right)} \]

Notação padrão: \(a\) está oposto a \(A\), \(b\) está oposto a \(B\) e \(c\) está oposto a \(C\).

Demonstração resumida e didática

Usaremos a Lei dos Senos e identidades trigonométricas de soma e diferença.

Pela Lei dos Senos, \( \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=2R \Rightarrow a=2R\sin A,\; b=2R\sin B\).
Então \[ \frac{a-b}{a+b}=\frac{\sin A-\sin B}{\sin A+\sin B}. \]
Use: \[ \sin A-\sin B=2\cos\!\left(\frac{A+B}{2}\right)\sin\!\left(\frac{A-B}{2}\right), \] \[ \sin A+\sin B=2\sin\!\left(\frac{A+B}{2}\right)\cos\!\left(\frac{A-B}{2}\right). \]
Logo, \[ \frac{a-b}{a+b} =\frac{\tan\!\left(\dfrac{A-B}{2}\right)}{\tan\!\left(\dfrac{A+B}{2}\right)}. \]

As outras duas formas seguem por simetria, trocando os pares \((A,B)\rightarrow(A,C)\) e \((A,B)\rightarrow(B,C)\).

Quando usar a Lei das Tangentes?

Para obter \(A-B\), \(A-C\) ou \(B-C\) quando se conhece um par de lados e o terceiro ângulo (pois \(A+B=180^\circ-C\) etc.).
Em problemas que envolvem diferenças de ângulos de forma natural.
Como alternativa às Leis dos Senos e dos Cossenos quando essas ficam algébrica ou numericamente menos convenientes.

Dica: muitas vezes é prático primeiro achar \( \dfrac{A+B}{2} \) ou \( \dfrac{B+C}{2} \) usando a soma dos ângulos internos do triângulo (180°) e, então, isolar \( \dfrac{A-B}{2} \) com a fórmula.

Exemplos resolvidos (passo a passo)

Exemplo 1 — encontrando \(A-B\)

Dados \(a=8\), \(b=5\) e \(C=60^\circ\). Encontre \(A-B\).

\[
\frac{a-b}{a+b}=\frac{8-5}{8+5}=\frac{3}{13}
\]
\[
A+B=180^\circ-C=120^\circ \Rightarrow \frac{A+B}{2}=60^\circ
\]
\[
\frac{3}{13}=\frac{\tan\!\left(\dfrac{A-B}{2}\right)}{\tan 60^\circ}
\Rightarrow \tan\!\left(\frac{A-B}{2}\right)=\frac{3}{13}\cdot\sqrt{3}
\]
\[
\frac{A-B}{2}=\arctan\!\left(\frac{3\sqrt{3}}{13}\right)
\;\Rightarrow\; A-B \approx 2\,\arctan\!\left(\frac{3\sqrt{3}}{13}\right)\;(\text{em graus})
\]

Se desejar estimar \(A\) e \(B\) individualmente, use também a Lei dos Senos após obter \(A-B\).

Exemplo 2 — forma \((b,c)\)

Dados \(b=10\), \(c=14\) e \(A=70^\circ\). Encontre \(B-C\).

\[
\frac{b-c}{b+c}=\frac{10-14}{10+14}=-\frac{4}{24}=-\frac{1}{6}
\]
\[
B+C=180^\circ-A=110^\circ \Rightarrow \frac{B+C}{2}=55^\circ
\]
\[
-\frac{1}{6}=\frac{\tan\!\left(\dfrac{B-C}{2}\right)}{\tan 55^\circ}
\Rightarrow \tan\!\left(\frac{B-C}{2}\right)=-\frac{1}{6}\tan 55^\circ
\]
\[
\frac{B-C}{2}=\arctan\!\left(-\frac{\tan 55^\circ}{6}\right)
\;\Rightarrow\; B-C \approx 2\,\arctan\!\left(-\frac{\tan 55^\circ}{6}\right)
\]

Comparação rápida com outras leis

Lei	Relação	Quando costuma ser melhor
Lei dos Senos	\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)	Quando há um lado conhecido com seu ângulo oposto, ou dois ângulos + um lado.
Lei dos Cossenos	\(a^2=b^2+c^2-2bc\cos A\) (cíclica)	Quando se conhece dois lados e o ângulo entre eles (ou os 3 lados).
Lei das Tangentes	\(\dfrac{a-b}{a+b}=\dfrac{\tan\!\left(\frac{A-B}{2}\right)}{\tan\!\left(\frac{A+B}{2}\right)}\) (e variantes)	Quando aparecem diferenças de lados/ângulos ou é conveniente usar meias-somas/meias-diferenças.

Exercícios de múltipla escolha (com gabarito no abre/fecha)

1) Em \(ABC\), \(a=9\), \(b=6\) e \(C=40^\circ\). Qual é o valor aproximado de \(A-B\)?

A) \(6^\circ\) B) \(10^\circ\) C) \(14^\circ\) D) \(18^\circ\)

Solução (passo a passo):

\[ \frac{a-b}{a+b}=\frac{9-6}{9+6}=\frac{3}{15}=\frac{1}{5} \]
\[ A+B=180^\circ-40^\circ=140^\circ \Rightarrow \frac{A+B}{2}=70^\circ \]
\[ \frac{1}{5}=\frac{\tan\!\left(\frac{A-B}{2}\right)}{\tan 70^\circ} \Rightarrow \tan\!\left(\frac{A-B}{2}\right)=\frac{1}{5}\tan 70^\circ \]
\[ \frac{A-B}{2}\approx \arctan\!\left(\frac{\tan 70^\circ}{5}\right) \Rightarrow A-B \approx 2\,\arctan\!\left(\frac{\tan 70^\circ}{5}\right)\approx 14^\circ \]

Gabarito: C

2) Se \(a=b\), então (assinale a correta):

A) \(A=B\) B) \(A=C\) C) \(B=C\) D) \(A=B=C\)

Solução: Da fórmula \(\displaystyle \frac{a-b}{a+b}=\frac{\tan\left(\frac{A-B}{2}\right)}{\tan\left(\frac{A+B}{2}\right)}\), se \(a=b\) então o lado esquerdo é \(0\), logo \(\tan\left(\frac{A-B}{2}\right)=0 \Rightarrow A=B\).

Gabarito: A

3) Em \(ABC\), \(b=10\), \(c=14\) e \(A=70^\circ\). Estime \(B-C\).

A) \(\approx -10^\circ\) B) \(\approx -6^\circ\) C) \(\approx -3^\circ\) D) \(\approx -1^\circ\)

\[ \frac{b-c}{b+c}=\frac{10-14}{24}=-\frac{1}{6},\quad B+C=110^\circ\Rightarrow\frac{B+C}{2}=55^\circ \]
\[ -\frac{1}{6}=\frac{\tan\!\left(\frac{B-C}{2}\right)}{\tan 55^\circ} \Rightarrow \tan\!\left(\frac{B-C}{2}\right)=-\frac{\tan 55^\circ}{6} \] Aproximando, obtemos \(B-C\approx -10^\circ\).

Gabarito: A

Erros comuns e boas práticas

Esquecer que \(A+B+C=180^\circ\): isso dá acesso direto a \(\dfrac{A+B}{2}\), \(\dfrac{A+C}{2}\) ou \(\dfrac{B+C}{2}\).
Usar graus e radianos misturados: mantenha uma única unidade ao calcular tangentes e arctangentes.
Ângulos obtusos: atenção ao quadrante de \(\arctan\) — valide com o contexto geométrico do triângulo.