Teorema do Ângulo Externo — \( \alpha + \beta = \theta \)

O ângulo externo de um triângulo é igual à soma dos dois ângulos internos não adjacentes. Use essa ideia junto com a Soma dos Ângulos Internos para resolver questões rápidas de geometria.

Definição: O Teorema do Ângulo Externo afirma que o ângulo externo de um triângulo é igual à soma dos dois ângulos internos não adjacentes:

\( \theta = \alpha + \beta \)

Essa propriedade está diretamente relacionada à Soma dos Ângulos Externos do Triângulo, onde a soma de todos os ângulos externos é sempre \(360^\circ\).

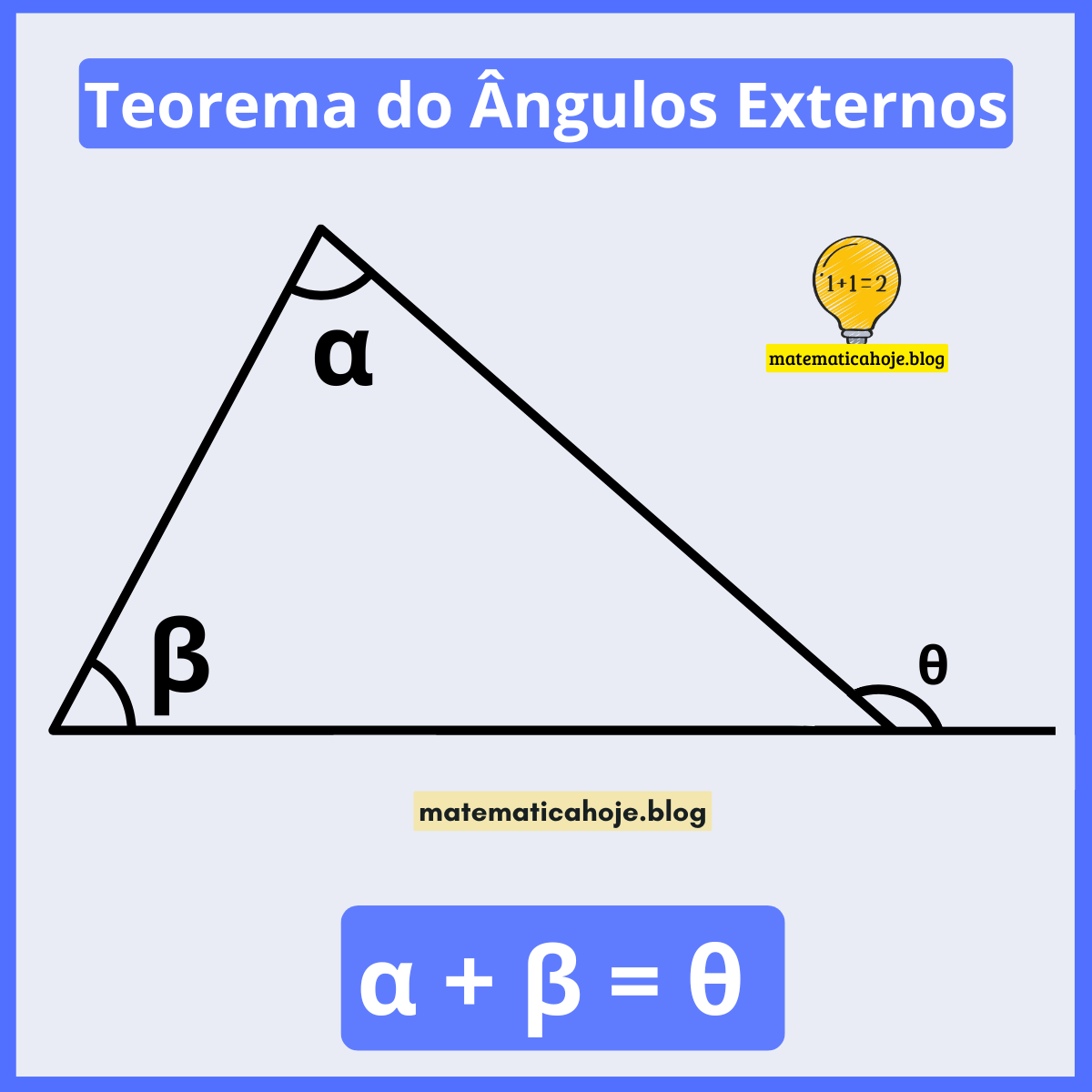
Teorema do Ângulo Externo: α + β = θ — Imagem: matematicaoje.blog — ângulo externo \( \theta \) é a soma de \( \alpha \) e \( \beta \).

Prova do Teorema

Sabemos que a Soma dos Ângulos Internos de um triângulo é \(180^\circ\): \( \alpha + \beta + \gamma = 180^\circ \).

O ângulo externo \( \theta \), adjacente a \( \gamma \), é suplementar a ele:

\(\theta = 180^\circ – \gamma\)
\(\gamma = 180^\circ – (\alpha + \beta)\)
\(\theta = 180^\circ – [180^\circ – (\alpha + \beta)]\)
\(\theta = \alpha + \beta\)

Mapas Mentais de Matemática

Visualize de forma clara os teoremas e propriedades de triângulos, além das regras de sinais e operações com inteiros.

Ver Mapas Mentais

Exemplos resolvidos

Exemplo 1 — Encontre o ângulo externo

Sabendo que \( \alpha = 45^\circ \) e \( \beta = 55^\circ \), calcule \( \theta \).

\(\theta = \alpha + \beta\)
\(\theta = 45^\circ + 55^\circ\)
\(\theta = 100^\circ\)

Exemplo 2 — Determine um ângulo interno

Um ângulo externo mede \( 130^\circ \) e um dos ângulos internos não adjacentes mede \( 70^\circ \). Qual o outro interno?

\(\theta = \alpha + \beta\)
\(130^\circ = 70^\circ + x\)
\(x = 60^\circ\)

Baixe o eBook Gratuito de Fórmulas Matemáticas

Revisão completa de fórmulas de triângulos, ângulos, potências e operações com números inteiros.

Baixar Grátis

Exercícios

1) Discursiva — Painel triangular

Os ângulos internos não adjacentes medem \( 35^\circ \) e \( 65^\circ \). Calcule o ângulo externo \( \theta \).

Ver solução

\(\theta = 35^\circ + 65^\circ = 100^\circ\)

2) Múltipla escolha — Construção

O ângulo externo mede \( 120^\circ \) e um dos internos não adjacentes mede \( 50^\circ \). O outro mede:

\(60^\circ\)
\(70^\circ\)
\(80^\circ\)
\(90^\circ\)

Mostrar resposta

\(120 = 50 + x\) \(x = 70^\circ\)

Resposta: Letra B.

Conclusão

O Teorema do Ângulo Externo é uma ferramenta essencial para resolver triângulos. Ele complementa a Soma dos Ângulos Internos e a Soma dos Ângulos Externos, formando a base para muitos problemas de geometria.

Estude também com o eBook Gratuito de Fórmulas Matemáticas e os Mapas Mentais de Matemática.