Tipos de Ângulos: Agudo, Reto, Obtuso e Raso
Este guia reúne, em um só lugar, tudo o que você precisa saber sobre os quatro ângulos clássicos da geometria: agudo, reto, obtuso e raso. Trazemos definições claras, propriedades, comparações, imagens, exemplos e um bloco de exercícios com gabarito.
Visão geral rápida
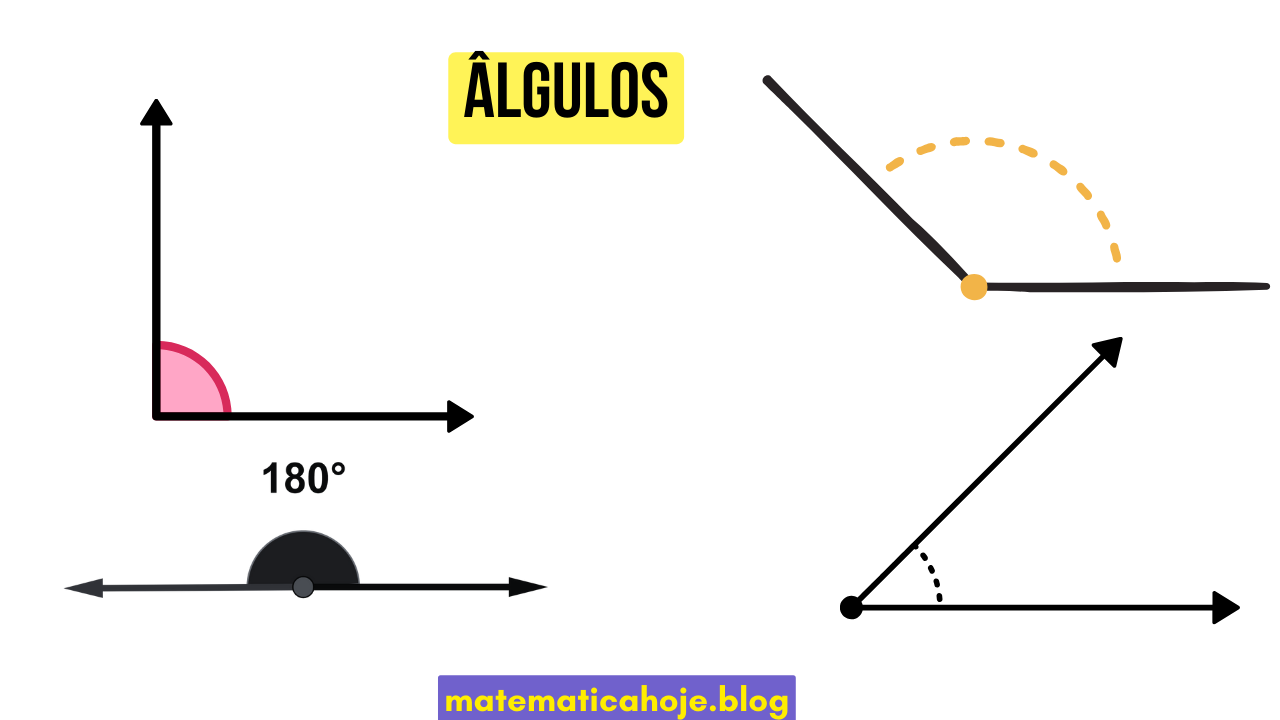
| Tipo | Definição | Intervalo | Exemplos |
|---|---|---|---|
| Agudo | Ângulo “pequeno” | \(0^\circ < \widehat{x} < 90^\circ\) | 30°, 45°, 72° |
| Reto | Ângulo de 90° | \(\widehat{x}=90^\circ\) | cantos de quadrados/retângulos |
| Obtuso | Ângulo “largo” | \(90^\circ < \widehat{x} < 180^\circ\) | 100°, 120°, 150° |
| Raso | Meia volta | \(\widehat{x}=180^\circ\) | ponteiros às 6h; linha reta |
1) Ângulo Agudo
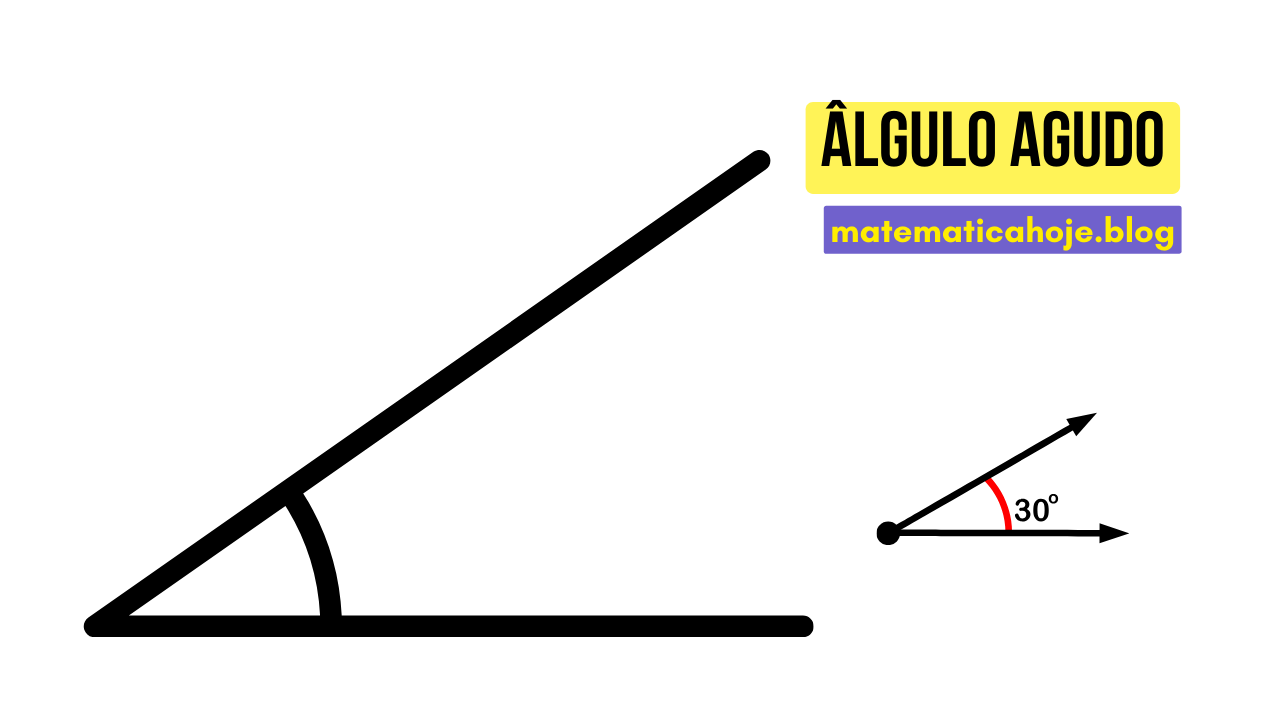
- Em todo triângulo retângulo, os dois ângulos que não são o reto são agudos e somam \(90^\circ\).
- Complemento de um ângulo agudo: \(90^\circ-\widehat{x}\).
2) Ângulo Reto
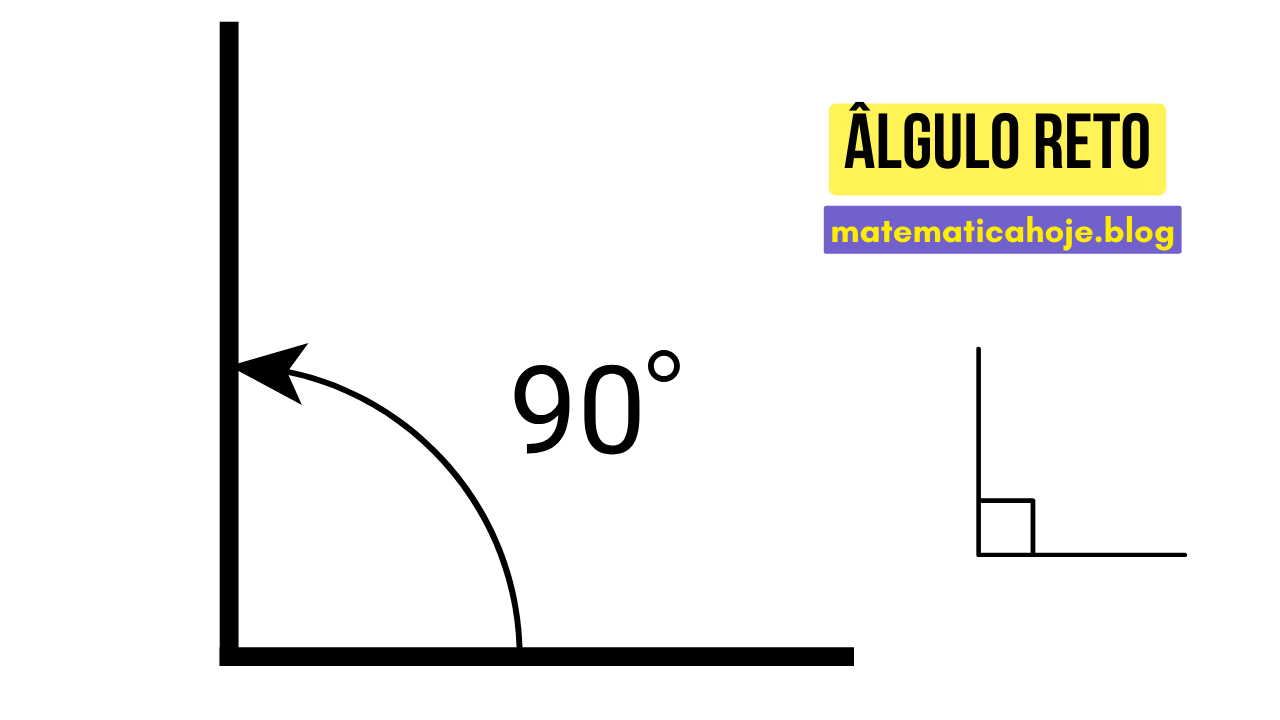
- Formado por retas perpendiculares.
- Dois ângulos retos somam um ângulo raso (180°).
3) Ângulo Obtuso
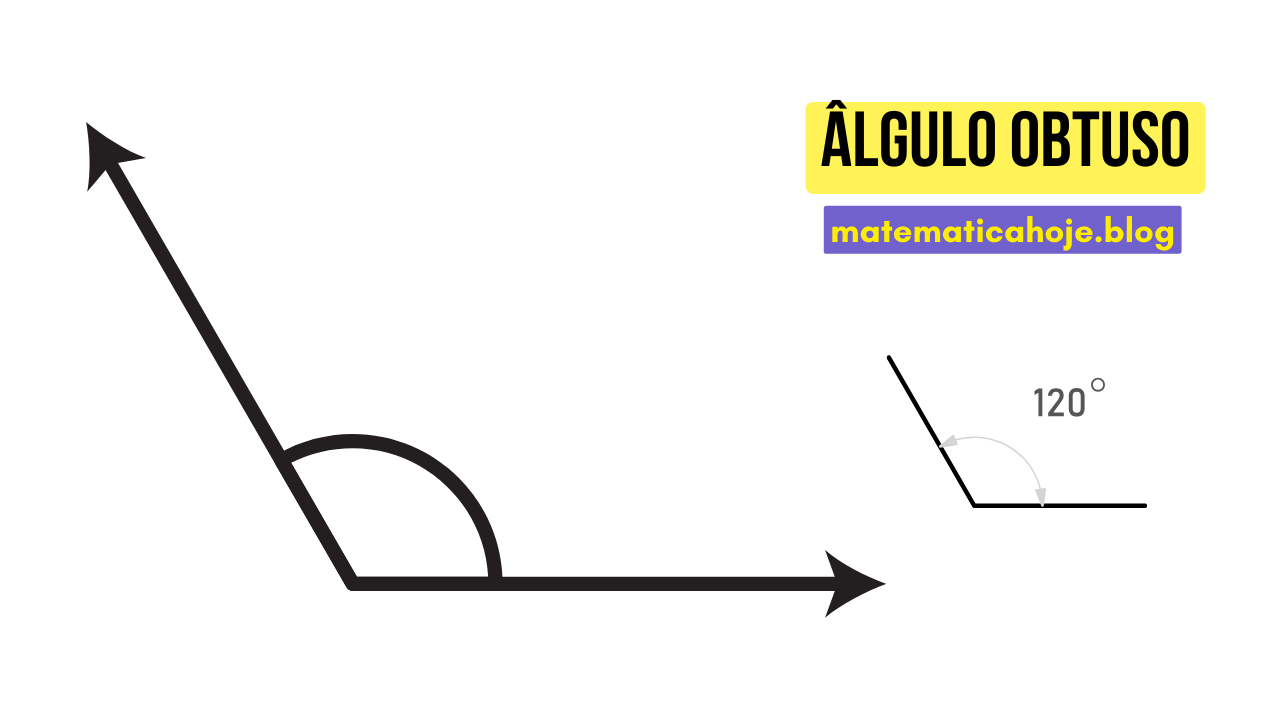
- Em um triângulo qualquer, no máximo um ângulo pode ser obtuso.
- Para \(\widehat{x}\) obtuso: \(\cos \widehat{x} < 0\).
4) Ângulo Raso
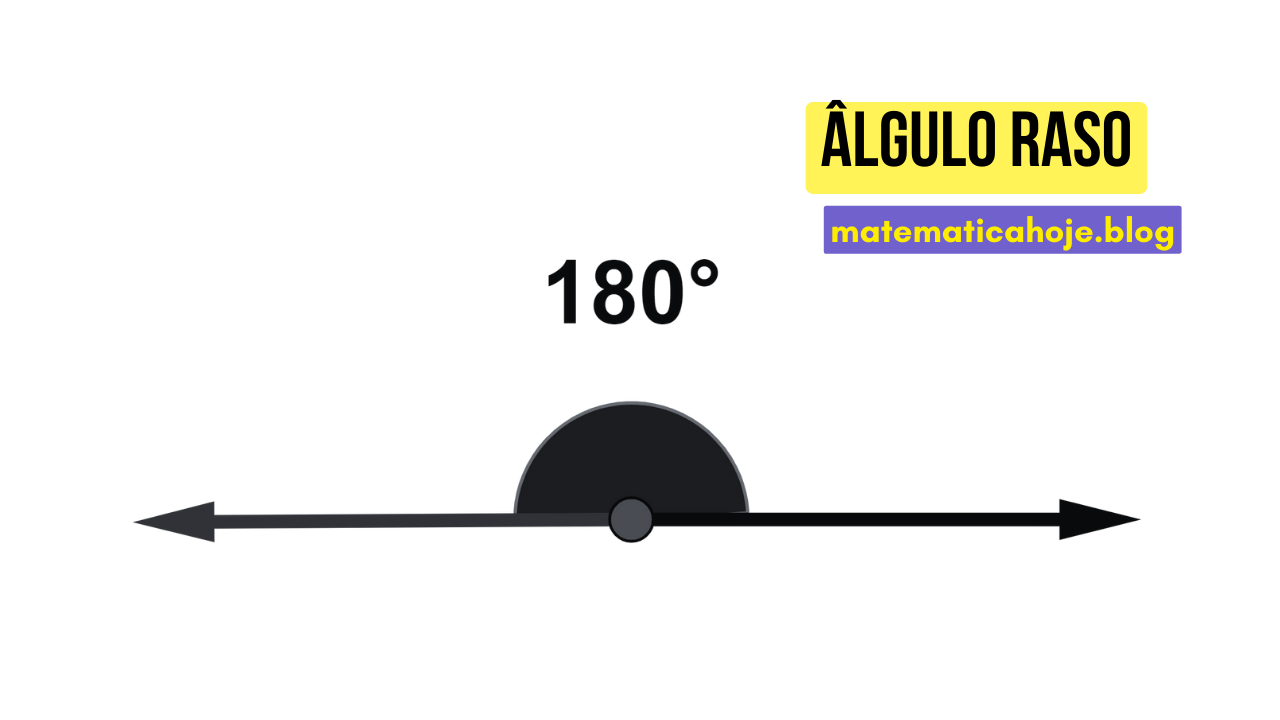
- Equivale a meia volta (linha reta).
- Útil para raciocínios de geometria com retas colineares.
Comparações e relações úteis
- Classificação por medida: Agudo < Reto < Obtuso < Raso.
- Ângulos complementares somam 90°; suplementares somam 180°.
- Em qualquer triângulo: \(\widehat{A}+\widehat{B}+\widehat{C}=180^\circ\) clássico
📘 Exercícios (múltipla escolha) — com solução
1) Qual opção não representa um ângulo agudo?
- 37°
- 58°
- 89°
- 95°
Ver solução
Agudo < 90°. 95° é obtuso.
2) Em um triângulo, dois ângulos medem 35° e 55°. Classifique o terceiro.
- Agudo
- Reto
- Obtuso
- Raso
Ver solução
Somam 90°, então o terceiro é 90° → reto.
3) Se um ângulo é suplementar de 46°, sua classificação é:
- Agudo
- Reto
- Obtuso
- Raso
Ver solução
Suplementar: 180° − 46° = 134° → obtuso.
4) Dois ângulos complementares medem \(x\) e \(2x\). Então \(x\) vale:
- 20°
- 30°
- 35°
- 45°
Ver solução
x + 2x = 90° → 3x = 90° → x = 30°.
5) Qual das alternativas descreve corretamente um ângulo raso?
- Maior que 90° e menor que 180°
- Menor que 90°
- Igual a 90°
- Igual a 180°
Ver solução
Definição de ângulo raso: 180°.
6) Em um triângulo isósceles, a base mede 50° em um vértice. Os outros dois ângulos são iguais e somam 130°. Cada um mede:
- 55° (agudos)
- 65° (obtusos? não, ainda < 90°)
- 70°
- 40°
Ver solução
180° − 50° = 130°. Dividindo igualmente: 65° e 65° (agudos).
7) Um triângulo tem um ângulo de 118°. Sobre os outros dois ângulos, podemos afirmar que:
- Ambos são obtusos
- Ambos são agudos
- Um é reto e outro agudo
- Um é raso e outro agudo
Ver solução
Somam 62°. Como cada um < 90°, ambos são agudos.
8) Um par de ângulos suplementares é (assinale a alternativa correta):
- 35° e 45°
- 60° e 60°
- 120° e 60°
- 70° e 10°
Ver solução
Suplementares somam 180°. 120° + 60° = 180°.
9) O complemento de um ângulo obtuso:
- Existe e é obtuso
- Existe e é agudo
- Não existe
- É reto
Ver solução
Complementares somam 90°. Como obtuso > 90°, não há complemento no conjunto dos ângulos positivos.
10) Qual alternativa contém a sequência correta: (agudo, reto, obtuso, raso)?
- \(0^\circ\), \(45^\circ\), \(120^\circ\), \(270^\circ\)
- \(10^\circ\), \(180^\circ\), \(100^\circ\), \(90^\circ\)
- \(45^\circ\), \(90^\circ\), \(135^\circ\), \(180^\circ\)
- \(30^\circ\), \(60^\circ\), \(150^\circ\), \(210^\circ\)
Ver solução
Agudo (<90), Reto (=90), Obtuso (entre 90 e 180), Raso (=180).
Links úteis
📚 Materiais recomendados
Complete seus estudos com os recursos do Matemática Hoje:
Este artigo integra e resume os quatro posts individuais, com linkagem interna para aprofundamento.





















