Transformações de Funções

Transformações de Funções (Translações): guia completo com exemplos e exercícios

Transformações de Funções: translações no eixo x e no eixo y com exemplos e exercícios

Neste guia você aprende, de forma simples, como **mover** o gráfico de uma função para **cima/baixo** e **direita/esquerda**. Essa habilidade aparece muito em **matemática básica**, **funções no ensino médio** e nas provas do **ENEM**. Vamos usar as notações: \(g(x)=f(x)+a\), \(g(x)=f(x)-a\), \(g(x)=f(x-a)\) e \(g(x)=f(x+a)\).

📌 Mapas Mentais de Matemática

Revisão visual de funções, gráficos, regras de sinais, porcentagem, estatística e muito mais.

Quero meus Mapas Mentais

📕 eBook Gratuito de Fórmulas Matemáticas

Baixe o PDF com as principais fórmulas para consultas rápidas durante os estudos.

Baixar grátis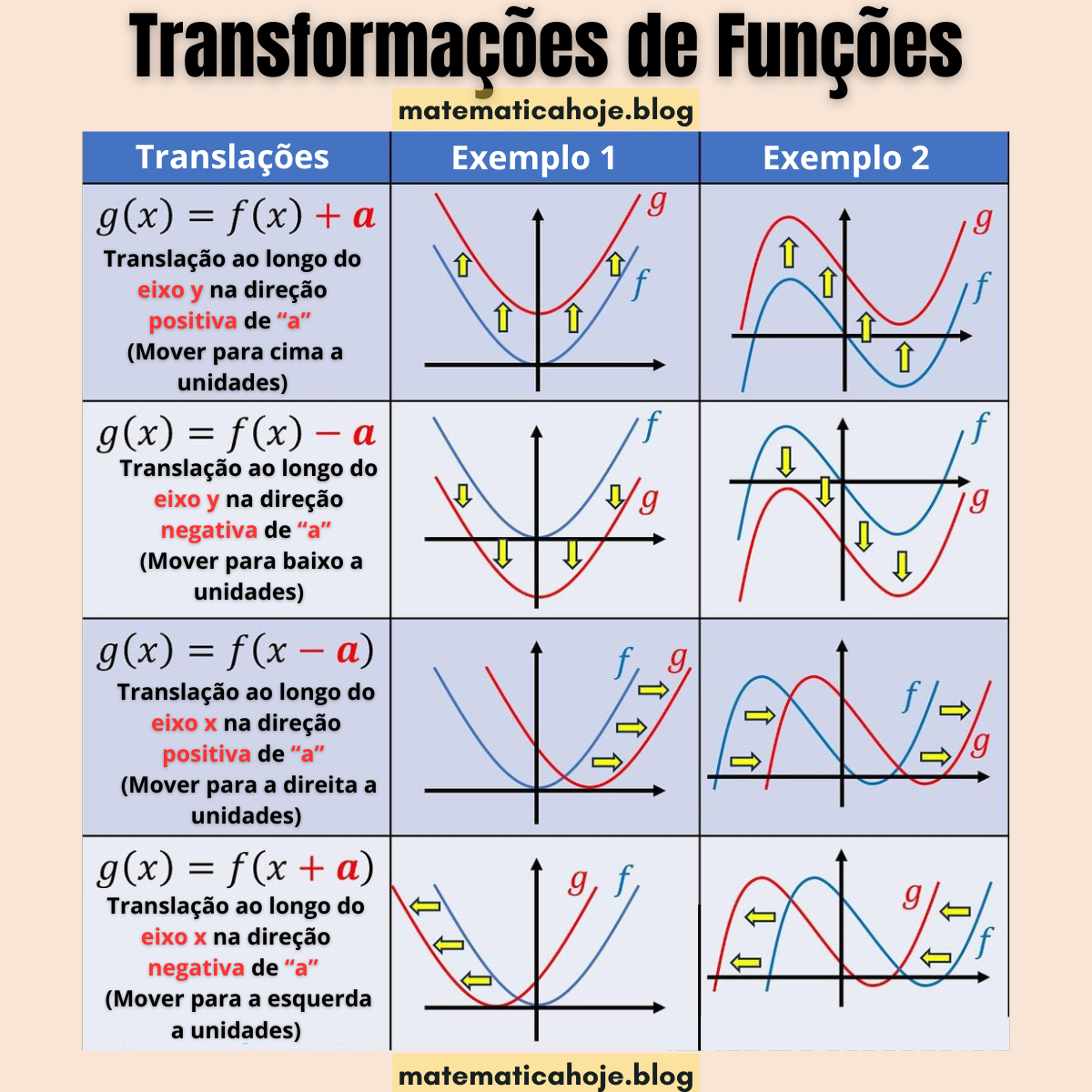
Transformações de Funções: translações nos eixos x e y – Matemática Hoje

1) O que é uma translação de função?

Translação é uma **mudança de posição** do gráfico sem alterar sua forma. Em termos práticos, é “arrastar” o gráfico mantendo a curvatura.

Regras de translação (memorização rápida)

  • Para cima: \(g(x)=f(x)+a\) com \(a>0\).
  • Para baixo: \(g(x)=f(x)-a\) com \(a>0\).
  • Para a direita: \(g(x)=f(x-a)\) com \(a>0\).
  • Para a esquerda: \(g(x)=f(x+a)\) com \(a>0\).

Dica: Sinal **fora** de \(x\) move **no eixo y**; sinal **junto ao x** move **no eixo x** (e o sentido no eixo x é “invertido”: \(-a\) desloca para a direita).

SEO — buscas relacionadas: operações com números inteiros, regras de sinais, adição e subtração de inteiros, multiplicação e divisão com sinais, matemática básica, jogo de sinais, translações de gráficos, deslocamento de funções, transformação de funções no plano cartesiano.

2) Exemplos resolvidos passo a passo

Exemplo A — mover para cima: \(g(x)=f(x)+3\)

Dada \(f(x)=x^2-4x+1\), determine \(g(x)=f(x)+3\). \[ \begin{aligned} g(x) &= f(x) + 3 \\ &= (x^2 – 4x + 1) + 3 \\ &= x^2 – 4x + 4 \end{aligned} \] Forma canônica: \[ \begin{aligned} g(x) &= x^2 – 4x + 4 \\ &= (x-2)^2 \end{aligned} \] Conclusão: \[ \text{Vértice de } f:\ (2,-3) \\ \text{Vértice de } g:\ (2,0) \quad \text{(subiu 3 unidades)} \]

Exemplo B — mover para a direita: \(g(x)=f(x-2)\)

Seja \(f(x)=\sqrt{x}\). Então: \[ \begin{aligned} g(x) &= f(x-2) \\ &= \sqrt{x-2} \end{aligned} \] O domínio: \[ \begin{aligned} x-2 &\ge 0 \\ x &\ge 2 \end{aligned} \] Conclusão: o gráfico inicia em \((2,0)\) — deslocou 2 para a direita.

Exemplo C — mover para a esquerda e para baixo: \(g(x)=f(x+1)-2\)

Dada \(f(x)=|x|\): \[ \begin{aligned} g(x) &= f(x+1) – 2 \\ &= |x+1| – 2 \end{aligned} \] Vértice de \(f\): \((0,0)\). \\ Vértice de \(g\): \((-1,-2)\) — 1 à esquerda e 2 para baixo.

Exemplo D — seno transladado: \(g(x)=\sin(x-\pi/3)+1\)

\[ \begin{aligned} g(x) &= \sin\!\left(x-\frac{\pi}{3}\right) + 1 \\ \text{Deslocamento em } x: &\ \frac{\pi}{3}\ \text{(direita)} \\ \text{Deslocamento em } y: &\ 1\ \text{(para cima)} \end{aligned} \] A amplitude e o período não mudam; apenas a posição do gráfico.

🎯 Mapas Mentais de Matemática (versão completa)

Transforme este conteúdo em revisão visual: gráficos, regras de sinais, porcentagem, progressões, geometria e muito mais.

Acessar Mapas Mentais

3) Exercícios propostos

Resolva primeiro. Em seguida, abra o toggle para conferir a solução passo a passo.

1) (Discursiva) Parabola “sobe”

A função base é \(f(x)=x^2-6x+5\). Construa \(g(x)=f(x)+4\) e informe o novo vértice.

Ver solução
\[ \begin{aligned} g(x) &= f(x)+4 \\ &= (x^2-6x+5)+4 \\ &= x^2-6x+9 \\ &= (x-3)^2 \end{aligned} \] Vértice de \(f\): \((3,-4)\). \\ Vértice de \(g\): \((3,0)\) — subiu 4 unidades.

2) (Múltipla escolha) Raiz deslocada

Se \(g(x)=\sqrt{x+5}\), o domínio correto é:

  1. \(x\ge -5\)
  2. \(x\le 5\)
  3. \(x\ge 5\)
  4. \(x\le -5\)
Mostrar resposta

Gabarito: A. Para \(\sqrt{x+5}\), exige-se \(x+5\ge0\Rightarrow x\ge-5\). (Translação 5 à esquerda.)

3) (Discursiva) Mover para a direita

Para \(f(x)=|x-2|\), determine \(g(x)=f(x-3)\). Qual é o ponto de mínimo?

Ver solução
\[ \begin{aligned} g(x) &= |(x-3)-2| \\ &= |x-5| \end{aligned} \] Mínimo de \(g\) em \(x=5\) com valor \(0\). O vértice moveu 3 unidades para a direita.

4) (Múltipla escolha) Seno com duas translações

Considere \(g(x)=\sin(x+\pi/4)-2\). Assinale a correta:

  1. Direita \(\pi/4\) e sobe 2
  2. Esquerda \(\pi/4\) e desce 2
  3. Direita \(\pi/4\) e desce 2
  4. Esquerda \(\pi/2\) e sobe 2
Mostrar resposta

Gabarito: B. \((x+\pi/4)\) desloca para a esquerda \(\pi/4\); “\(-2\)” desloca para baixo 2.

5) (Discursiva) Completando quadrado

\(f(x)=x^2\). Encontre \(g(x)=f(x-1)-3\) e o vértice do novo gráfico.

Ver solução
\[ \begin{aligned} g(x) &= (x-1)^2 – 3 \\ &= x^2 – 2x + 1 – 3 \\ &= x^2 – 2x – 2 \end{aligned} \] Vértice: \((1,-3)\) — direita 1 e para baixo 3.

6) (Múltipla escolha) Qual é a translação?

A partir de \(f(x)=\ln x\), obtém-se \(g(x)=\ln(x-4)+2\).

  1. Direita 4; sobe 2
  2. Esquerda 4; sobe 2
  3. Direita 2; sobe 4
  4. Direita 4; desce 2
Mostrar resposta

Gabarito: A. \((x-4)\) → direita 4; “+2” → para cima 2.

7) (Discursiva) Função cúbica

\(f(x)=x^3\). Determine a equação de \(g\) ao deslocar 2 para a esquerda e 1 para cima.

Ver solução
\[ \begin{aligned} g(x) &= f(x+2) + 1 \\ &= (x+2)^3 + 1 \end{aligned} \]

8) (Múltipla escolha) Domínio após translação

Para \(f(x)=\dfrac{1}{x}\), considere \(g(x)=f(x+1)\). O domínio de \(g\) é:

  1. \(x\in\mathbb{R}\)
  2. \(x\ne -1\)
  3. \(x\ne 1\)
  4. \(x\ge -1\)
Mostrar resposta

Gabarito: B. \(\dfrac{1}{x+1}\) é indefinida em \(x=-1\).

4) Checklist rápido para provas

  • Identifique se o termo que altera a função está **fora** (eixo y) ou **junto ao x** (eixo x).
  • No eixo x, lembre do **sentido invertido**: \(x-a\) → direita; \(x+a\) → esquerda.
  • Domínios e pontos notáveis (raízes, vértice, assíntotas) se movem com o gráfico.
  • Translação **não altera** a forma: amplitude, concavidade e período (quando existirem) permanecem.

📚 ENEM Matemática

Questões do ENEM resolvidas passo a passo, com foco em funções e interpretação de gráficos.

Estudar para o ENEM

📦 10 eBooks de Matemática

Conjunto premium com teoria, exemplos e listas — da matemática básica ao ensino médio.

Quero o pacote

📝 Banco de Questões de Matemática

Mais de 600 questões editáveis com solução. Ideal para simulados e revisões.

Acessar o banco

📕 eBook Gratuito de Fórmulas Matemáticas

Guarde no celular e consulte sempre que precisar.

Baixar agora

5) Conteúdos relacionados

Conclusão

Dominar as transformações de funções facilita a leitura de gráficos, acelera resoluções e ajuda muito em provas. Continue praticando com as listas e materiais gratuitos do Matemática Hoje.

Baixar eBook de Fórmulas Ver Mapas Mentais Seguir nosso canal no WhatsApp

Relacionadas

Sinal da função

Função bijetiva

Leitura e interpretação de gráficos

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube