Triângulos Congruentes
SEO discreto: triângulos congruentes, critérios LAL, ALA, LLL, RHC, CPCTC.
Definição e correspondência
Dois triângulos \( \triangle ABC \) e \( \triangle A’B’C’ \) são congruentes quando existe uma correspondência \(A\leftrightarrow A’\), \(B\leftrightarrow B’\), \(C\leftrightarrow C’\) que torna todos os lados e ângulos correspondentes iguais. Notação: \( \triangle ABC \cong \triangle A’B’C’ \).
Critérios clássicos (um abaixo do outro)
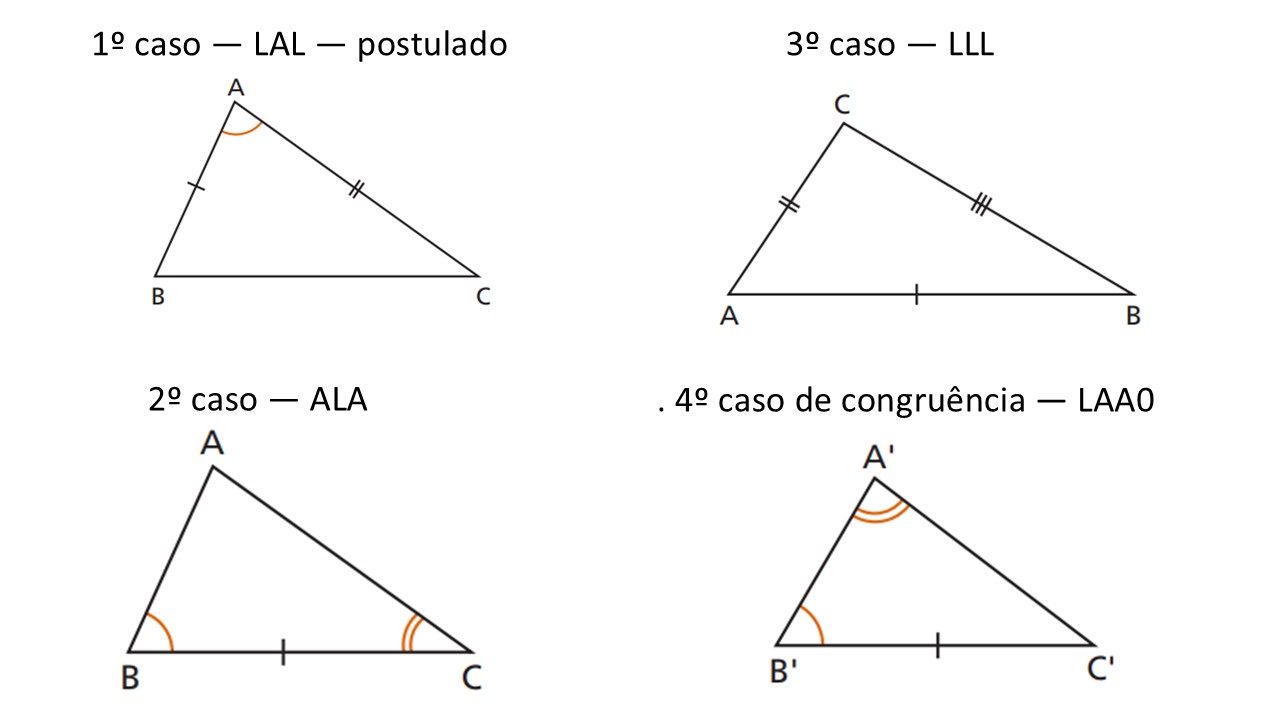
1) LAL — lado, ângulo, lado (ângulo entre os lados)
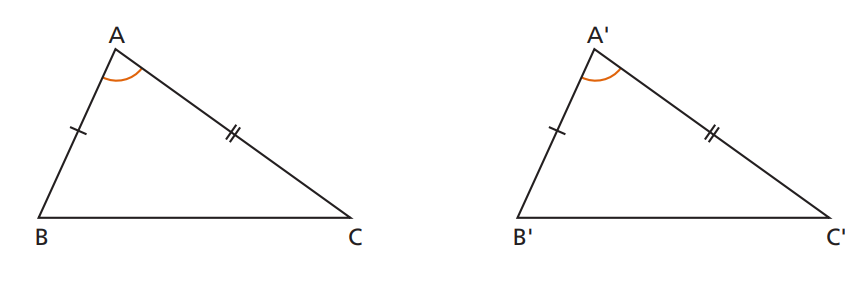
Se dois lados e o ângulo compreendido forem correspondentes e iguais, os triângulos são congruentes (LAL).
2) ALA — ângulo, lado, ângulo (lado entre os ângulos)
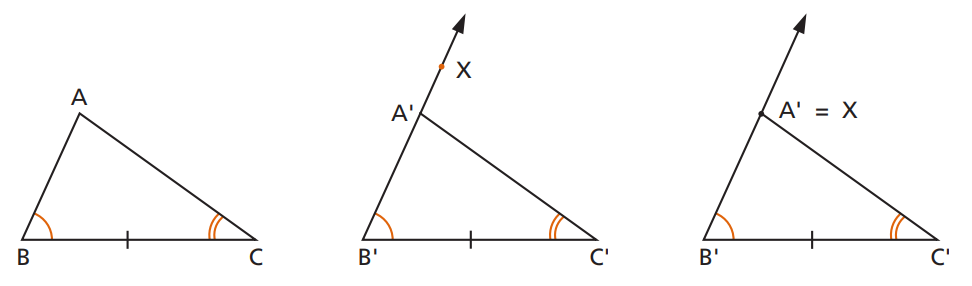
Se dois ângulos e o lado compreendido forem iguais, há congruência (ALA).
3) LLL — lado, lado, lado
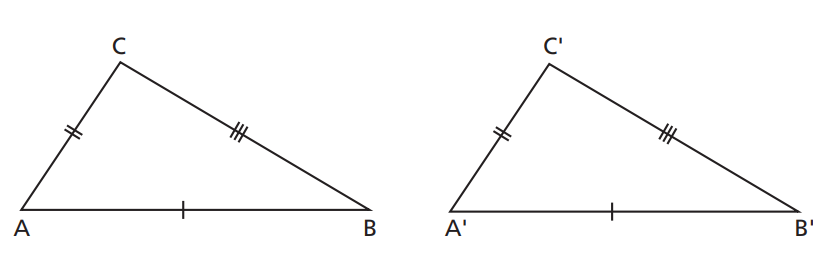
Se os três lados correspondentes são iguais, os triângulos são congruentes (LLL).
4) LAA (ou AAL) — dois ângulos e um lado não compreendido
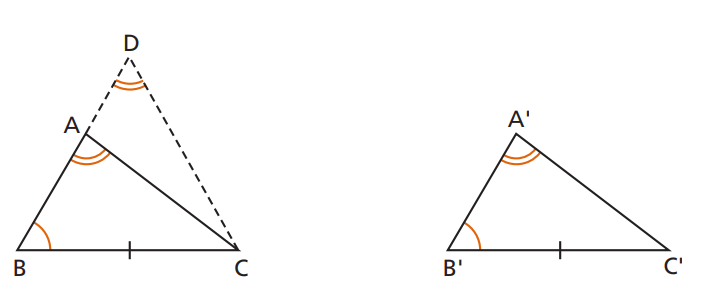
AAL também garante congruência, pois o terceiro ângulo fica determinado (reduz a ALA). Em triângulos retângulos, usa-se ainda RHC: hipotenusa e um cateto correspondentes iguais.
Exemplos resolvidos (abre/fecha)
Exemplo 1 — LAL. Em \( \triangle ABC \) e \( \triangle A’B’C’ \): \(AB=A’B’\), \(AC=A’C’\) e \( \angle BAC=\angle B’A’C’ \). Conclua e prove \(BC=B’C’\).
Mostrar solução
LAL ⇒ \( \triangle ABC \cong \triangle A’B’C’ \). CPCTC ⇒ \(BC=B’C’\).
Exemplo 2 — LLL. \(AB=DE=7\), \(BC=EF=9\), \(AC=DF=11\). Conclua e determine \( \angle A \) se \( \angle D=40^\circ \).
Mostrar solução
LLL ⇒ \( \triangle ABC \cong \triangle DEF \). CPCTC ⇒ \( \angle A=\angle D=40^\circ \).
Exemplo 3 — RHC. Dois triângulos retângulos têm hipotenusa 10 e um cateto 6 correspondentes. Mostre a congruência e calcule o outro cateto.
Mostrar solução
RHC ⇒ congruentes.
\(x^2+6^2=10^2\)
\(x^2+36=100\)
\(x^2=64\Rightarrow x=8\).
Exercícios de múltipla escolha
1) Quais critérios garantem congruência?
Mostrar solução
Resposta: D.
2) Se dois triângulos têm os três ângulos correspondentes iguais, então eles são:
Mostrar solução
Resposta: B (AAA ⇒ semelhança).
3) Em dois triângulos, \(AB=DE\), \(BC=EF\) e \( \angle B=\angle E \) (ângulo entre \(AB\) e \(BC\)). O critério é:
Mostrar solução
Resposta: B.
4) Em triângulos retângulos, hipotenusas iguais e um cateto correspondente igual implicam:
Mostrar solução
Resposta: C.
5) Qual conjunto é ambíguo e pode não garantir congruência?
Mostrar solução
Resposta: C.
6) Se \( \triangle ABC \cong \triangle A’B’C’ \) e \(AB=7\), \(BC=9\), \(CA=11\), então \(P_{A’B’C’}\) é:
Mostrar solução
Resposta: C (perímetro 27).
7) Em triângulos congruentes, \( \angle A = 50^\circ \) e \( \angle B’ = 60^\circ \). O valor de \( \angle C’ \) é:
Mostrar solução
Resposta: B (180 − 50 − 60).
8) Dois triângulos isósceles possuem lados da base iguais e o ângulo entre esse lado e um lado congruente adjacente é igual. O critério é:
Mostrar solução
Resposta: B.
9) Em dois triângulos, \( \angle A=\angle A’ \), \( \angle C=\angle C’ \) e \( AC=A’C’ \). O critério é:
Mostrar solução
Resposta: A.
10) Se \( \triangle ABC \cong \triangle A’B’C’ \) e \( \angle B=72^\circ \), \( \angle C’=48^\circ \), então \( \angle A \) vale:
Mostrar solução
Resposta: B (180 − 72 − 48 = 60).
Continue estudando
Triângulo retângulo Triângulo isósceles Triângulo equilátero Triângulo escaleno Tipos de triângulos Área de triângulo Pontos notáveis Incírculo e circunscrita
Materiais recomendados
Mapas Mentais de Matemática
Os quatro casos (LAL, ALA, LLL, RHC) em um só esquema — memorização rápida.
Quero os Mapas+600 Questões ENEM Matemática
Pratique congruência, semelhança e trigonometria com gabarito comentado.
Praticar agoraColeção 10 eBooks
Teoria objetiva + listas resolvidas: congruência, semelhança e aplicações.
Ver coleçãoBanco de Questões
Monte listas por assunto e acompanhe seu progresso (CPCTC, LAL, LLL…).
Acessar bancoCanais Oficiais
Receba novos artigos, exercícios e simulados no seu celular.
Entrar nos canais