Questão 11 – Geometria (USCS-SP)
Em um cartão quadrado \(ABCD\), de área igual a \(256 \, \text{cm}^2\), destaca-se uma região triangular \(ABP\), conforme mostra a figura.
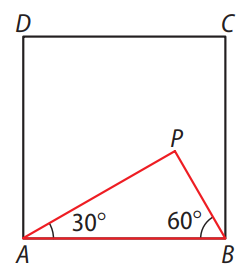
O perímetro da região delimitada pelo triângulo \(ABP\) é igual a:
- a) \(8(2 + \sqrt{2}) \, \text{cm}\).
- b) \(6(3 + \sqrt{3}) \, \text{cm}\).
- c) \(24 \sqrt{3} \, \text{cm}\).
- d) \(8(3 + \sqrt{3}) \, \text{cm}\).
- e) \(32 \sqrt{3} \, \text{cm}\).
Solução Passo a Passo:
1. Determinamos a medida do lado \(x\) do quadrado: \[ x^2 = 256 \quad \Rightarrow \quad x = 16 \, \text{cm}. \]
2. Considerando o triângulo \(ABP\), com ângulos de \(30^\circ\) e \(60^\circ\), temos: \[ \sin 30^\circ = \frac{BP}{AB} \quad \Rightarrow \quad BP = 8 \, \text{cm}, \] \[ \cos 30^\circ = \frac{AP}{AB} \quad \Rightarrow \quad AP = 8 \sqrt{3} \, \text{cm}. \]
3. Assim, o perímetro do triângulo \(ABP\) é: \[ P = AB + BP + AP = 16 + 8 + 8 \sqrt{3} = 8(3 + \sqrt{3}) \, \text{cm}. \]
Resposta final: alternativa d) \(8(3 + \sqrt{3}) \, \text{cm}\).
🔗 Acesse nossos Mapas Mentais
📘 Baixe nossos 10 eBooks de Matemática
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon












