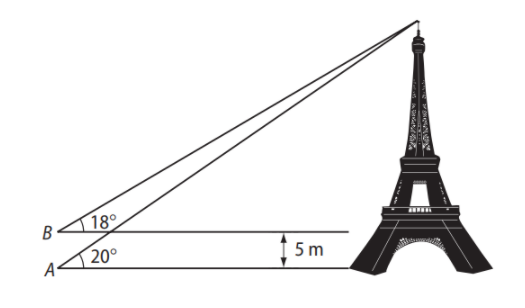
(UFAL) De um ponto \( A \), situado no mesmo nível da base de uma torre, o ângulo de elevação do topo da torre é de \( 20^\circ \). De um ponto \( B \), situado na mesma vertical de \( A \) e \( 5 \, \text{m} \) acima, o ângulo de elevação do topo da torre é de \( 18^\circ \). Qual a altura da torre? Dados: \( \tan 20^\circ \approx 0,36 \) e \( \tan 18^\circ \approx 0,32 \).
a) 42 m
b) 43 m
c) 44 m
d) 45 m
e) 46 m
Sejam \( h \) a altura da torre e \( d \) a distância do ponto \( A \) à base da torre. Aplicando a tangente nos dois ângulos:
Substituindo \( h \) da equação (I) na (II):
Substituindo \( d \) em (I):
Portanto, a altura da torre é 45 m (alternativa d).
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon











