O tronco de pirâmide é uma figura geométrica tridimensional da matemática obtida ao se cortar uma pirâmide por um plano paralelo à base, resultando em duas pirâmides, uma maior e uma menor. Neste artigo, exploraremos as propriedades e as fórmulas essenciais do tronco de pirâmide, utilizando as notações: (a) para a aresta da pirâmide menor, (A) para a aresta da pirâmide maior, (h) para a altura da pirâmide menor, (H) para a altura da pirâmide maior, (Ab) para a área da base menor, (AB) para a área da base maior, (vol) para o volume da pirâmide menor, e (VOL) para o volume da pirâmide maior.
Artigos Atualizados
Tronco de Pirâmide e Razões de Semelhança
Definições Básicas
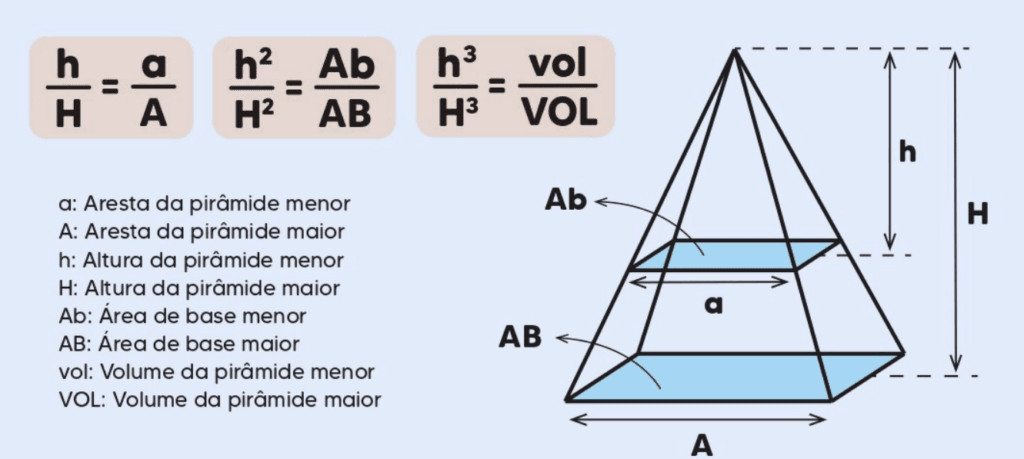
- Arestas da Pirâmide: (a) e (A) representam as arestas das bases da pirâmide menor e maior, respectivamente.
- Alturas da Pirâmide: (h) e (H) são as alturas das pirâmides menor e maior.
- Áreas das Bases: (Ab) e (AB) referem-se às áreas das bases menor e maior, respectivamente.
- Volumes: (vol) e (VOL) são os volumes das pirâmides menor e maior, respectivamente.
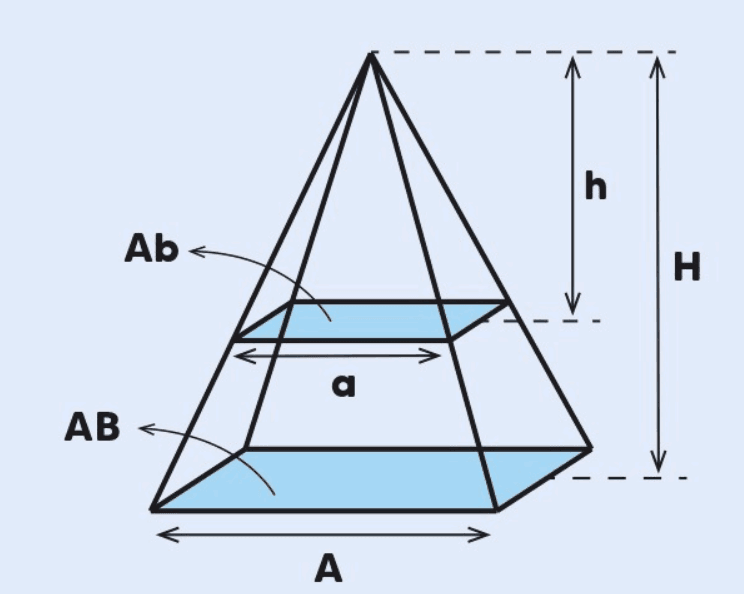
Propriedades do Tronco de Pirâmide
O tronco de pirâmide possui uma base maior e uma base menor, com suas faces laterais sendo trapézios. As propriedades geométricas relacionadas às dimensões da pirâmide maior e da menor podem ser expressas em termos de proporções.
Proporção das Arestas
As arestas das bases do tronco de pirâmide são proporcionais às alturas das pirâmides correspondentes:
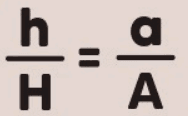
Essa relação indica que a razão entre as arestas das bases é a mesma que a razão entre as alturas das pirâmides.
Exemplo 1: Proporção das Arestas
Uma pirâmide truncada tem uma base maior com aresta A=10 cm e uma base menor com aresta a=6 cm. Se a altura da pirâmide maior é H=15 , qual é a altura h da pirâmide menor?
Resolução:
A relação entre as arestas e as alturas das pirâmides maior e menor é dada por:
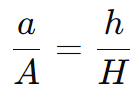
Substituindo os valores:
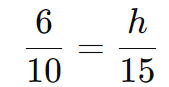
Resolvendo para h:
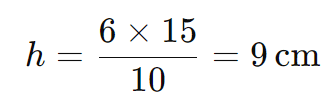
Resposta: A altura da pirâmide menor é 9 cm.
Proporção das Áreas
As áreas das bases do tronco de pirâmide também seguem uma proporção com base no quadrado das alturas:
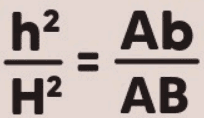
Isso reflete o fato de que as áreas das bases são proporcionais ao quadrado das alturas correspondentes.
Exemplo 2: Proporção das Áreas
Dado um tronco de pirâmide com área da base maior AB=64 cm2 e área da base menor Ab=36 cm2. Se a altura da pirâmide maior é H=12 , qual é a altura h da pirâmide menor?
Resolução:
A relação entre as áreas e as alturas das pirâmides maior e menor é dada por:
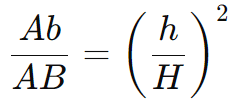
Substituindo os valores:
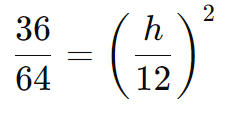
Simplificando a fração:
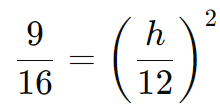
Extraindo a raiz quadrada dos dois lados:
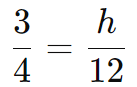
Resolvendo para h:
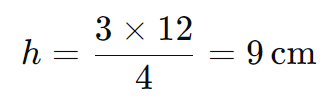
Resposta: A altura da pirâmide menor é 9 cm.
Proporção dos Volumes
Os volumes das pirâmides menor e maior estão relacionados pela proporção cúbica das alturas

Essa relação mostra que o volume de uma pirâmide é proporcional ao cubo da altura.
Exemplo 3: Proporção dos Volumes
Um tronco de pirâmide tem volumes VOL=200 cm3 para a pirâmide maior e vol=50 cm3 para a pirâmide menor. Se a altura da pirâmide maior é H=10 cm, qual é a altura h da pirâmide menor?
Resolução:
A relação entre os volumes e as alturas das pirâmides maior e menor é dada por:
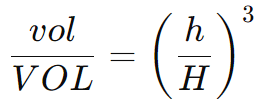
Substituindo os valores:
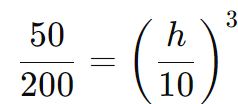
Simplificando a fração:
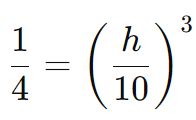
Extraindo a raiz cúbica dos dois lados:
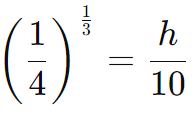
Calculando a raiz cúbica:
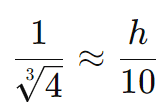
Resolvendo para h:
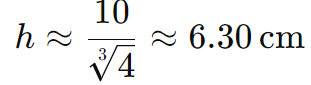
Resposta: A altura da pirâmide menor é aproximadamente 6.30 cm.
Fórmulas Importantes para o Tronco de Pirâmide
- Altura do Tronco de Pirâmide: A altura do tronco de pirâmide é a diferença entre as alturas das pirâmides maior e menor:
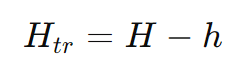
- Área Lateral do Tronco de Pirâmide: A área lateral do tronco de pirâmide pode ser calculada somando as áreas dos trapézios que formam as faces laterais.
- Volume do Tronco de Pirâmide: O volume do tronco de pirâmide é dado pela diferença entre os volumes da pirâmide maior e da pirâmide menor:
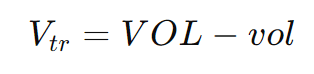
Cálculo do Volume do Tronco de Pirâmide: Fórmula e Intuição Geométrica
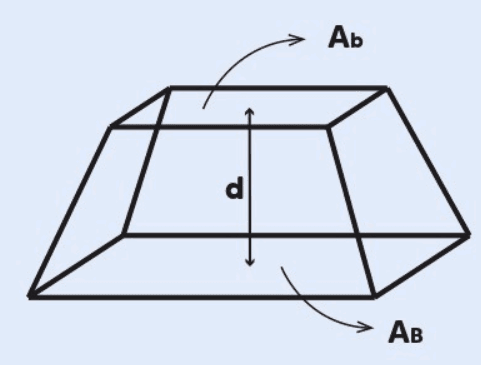
volume de um tronco de pirâmide é uma das propriedades mais importantes e pode ser calculado utilizando a fórmula que leva em consideração as áreas das bases maior e menor, bem como a altura do tronco. A fórmula geral para o volume Vt de um tronco de pirâmide é dada por:
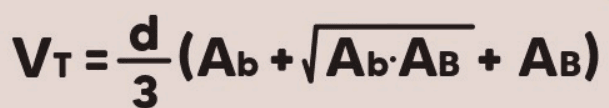
Onde:
- Ht é a altura do tronco de pirâmide, que é a distância perpendicular entre as duas bases.
- AB é a área da base maior.
- Ab é a área da base menor.
Explicação da Fórmula
A fórmula para o volume do tronco de pirâmide é baseada no princípio de que o volume de um tronco é equivalente ao volume de uma pirâmide maior subtraído o volume de uma pirâmide menor que foi “cortada” do topo. A média ponderada das áreas das duas bases, junto com a altura do tronco, determina o espaço tridimensional ocupado pelo tronco.
Exercício 4: Cálculo do Volume
Enunciado:
Um tronco de pirâmide tem uma base maior com área AB=100 cm2, uma base menor com área Ab=25 cm2, e uma altura Htr=12 cm. Calcule o volume do tronco de pirâmide.
Resolução:
A fórmula para o volume Vtr do tronco de pirâmide é:
Resolução:
A fórmula para o volume Vtr do tronco de pirâmide é:
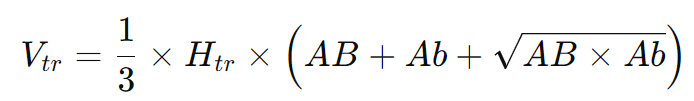
Substituindo os valores:
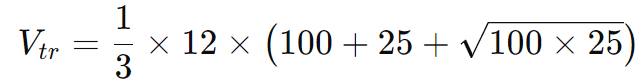
Calculando:
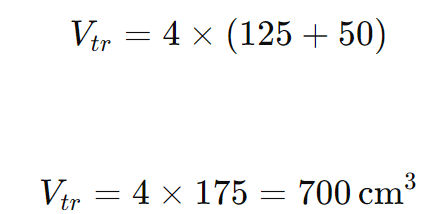
Resposta: O volume do tronco de pirâmide é 700 cm3.
Derivação e Intuição
- Média das Bases: A fórmula considera as áreas das duas bases AB e Ab, bem como a média geométrica
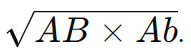
Essa média geométrica ajuda a levar em conta a variação de área entre as duas bases, proporcionando uma transição suave ao longo da altura do tronco.
- Altura do Tronco: A altura Ht do tronco é crucial para o cálculo, pois define a profundidade ao longo da qual a transição entre as duas bases ocorre.
Essa abordagem fornece uma forma precisa de calcular o volume do tronco de pirâmide, refletindo a geometria complexa do sólido de maneira simples e eficiente.
Resumo
Conclusão
O tronco de pirâmide é uma figura geométrica com diversas propriedades interessantes, especialmente no que diz respeito às proporções entre as dimensões das pirâmides que o compõem. Compreender as relações entre arestas, alturas, áreas e volumes é essencial para explorar plenamente as características desse sólido. As fórmulas e proporções apresentadas fornecem uma base sólida para a análise geométrica do tronco de pirâmide e suas aplicações em diferentes contextos.
Leia também
O Cubo: Propriedades e Fórmulas Essenciais
O Paralelepípedo: Propriedades e Fórmulas Essenciais
Pirâmides: Propriedades, Fórmulas e Aplicações
Tetraedro Regular: Propriedades, Fórmulas e Aplicações
Tronco de Pirâmide: Propriedades, Fórmulas e Proporções
Cilindro: Conceitos e Cálculos
Cone: Tudo o Que Você Precisa Saber
Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão