Tronco de Pirâmide: Conceitos, Fórmulas, Exemplos e Exercícios
Guia completo com volume, áreas, casos regulares, aplicações e questões com solução em abre/fecha.
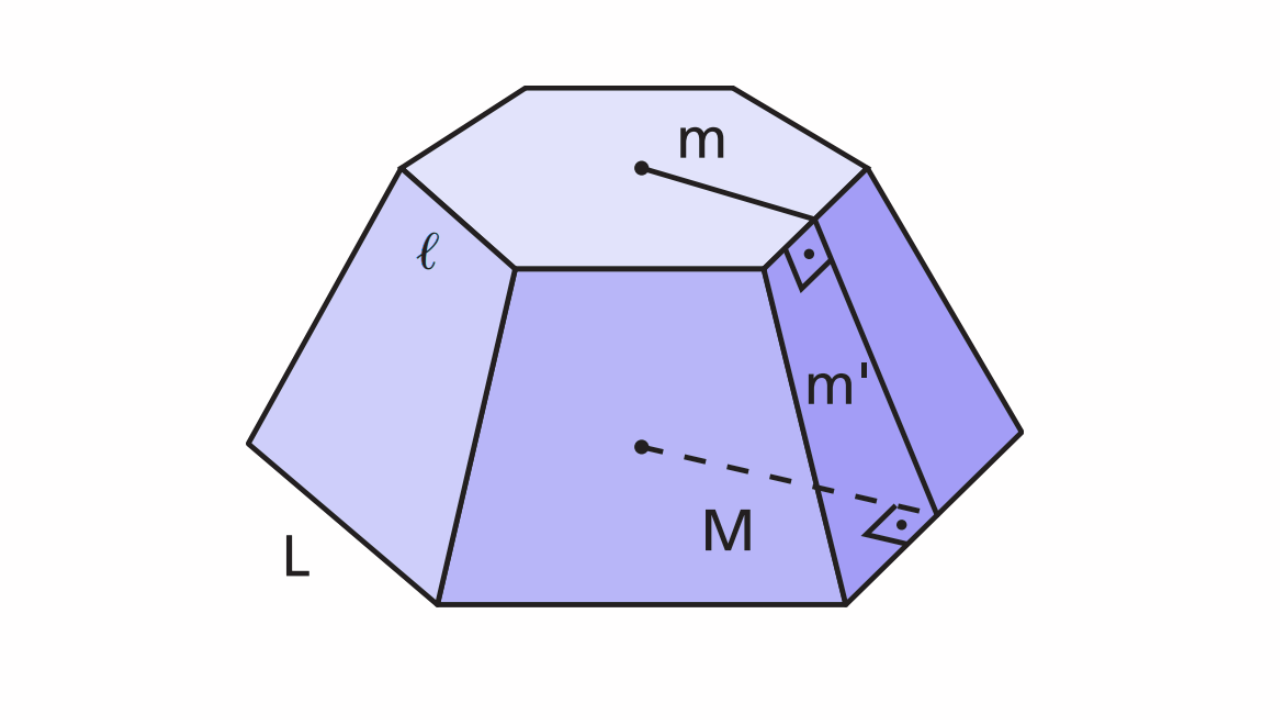
O tronco de pirâmide surge ao cortar uma pirâmide por um plano paralelo à sua base, removendo o topo. O sólido resultante tem duas bases paralelas — uma maior (da pirâmide original) e outra menor (a seção do corte) — e faces laterais em forma de trapézios. É conteúdo recorrente em provas, inclusive no ENEM, e em listas de exercícios.
Nomeclatura usada neste artigo
- h: altura (distância entre os planos das bases).
- B e b: áreas das bases maior e menor, respectivamente.
- P e p: perímetros das bases maior e menor.
- g: apótema (altura inclinada das faces laterais) em tronco de pirâmide regular.
Em troncos não regulares, a área lateral é a soma das áreas dos trapézios; no caso regular, existe uma fórmula compacta com g.
Fórmulas essenciais
Volume
\( V \;=\; \dfrac{h}{3}\,\big(B + b + \sqrt{B\,b}\big) \)
Válida para qualquer tronco de pirâmide (regular ou não), pois depende apenas de áreas das bases e da altura.
Área lateral (tronco regular)
\( A_L \;=\; \dfrac{(P + p)\,g}{2} \)
Aqui, todas as faces laterais são trapézios isósceles com mesma apótema \(g\).
Área total
\( A_T \;=\; A_L + B + b \)
Dicas rápidas
- Sem semelhança direta? Calcule \(B\) e \(b\) a partir dos polígonos das bases (ex.: quadrado, hexágono etc.).
- Regular Se as bases são regulares e de mesmo número de lados, os lados são proporcionais: \( \dfrac{\text{lado da base menor}}{\text{lado da base maior}} = k \Rightarrow \dfrac{b}{B} = k^2 \).
- Altura inclinada Em muitos problemas, \(g\) é fornecida. Quando não, use relações métricas do sólido (Pitágoras) conforme o caso.
Exemplo resolvido passo a passo
Tronco de pirâmide quadrada com:
- Base maior: lado \(10\,\text{cm}\) → \( B = 10^2 = 100\,\text{cm}^2 \)
- Base menor: lado \(6\,\text{cm}\) → \( b = 6^2 = 36\,\text{cm}^2 \)
- Altura: \( h = 8\,\text{cm} \)
\( V = \dfrac{8}{3}\,\big(100 + 36 + \sqrt{100\cdot 36}\big) \)
\( V = \dfrac{8}{3}\,(100 + 36 + 60) = \dfrac{8}{3}\cdot 196 \)
\( V \approx 522{,}6\ \text{cm}^3 \)
Aplicações
- Arquitetura e engenharia (pilares, reservatórios, telhados).
- Modelagem e estimativa de materiais.
- Problemas típicos de provas de ensino médio e concursos.
Exercícios (múltipla escolha)
1) Volume com bases quadradas
Um tronco de pirâmide quadrada tem lados das bases \(12\,\text{cm}\) e \(8\,\text{cm}\) e altura \(9\,\text{cm}\). Calcule o volume.
- \(864\,\text{cm}^3\)
- \(912\,\text{cm}^3\)
- \(936\,\text{cm}^3\)
- \(960\,\text{cm}^3\)
\(B=12^2=144,\ b=8^2=64,\ h=9\).
\(V=\dfrac{9}{3}(144+64+\sqrt{144\cdot64})=3(208+96)=\mathbf{912}\ \text{cm}^3\). Alternativa B.
2) Área lateral (tronco regular)
Num tronco de pirâmide regular hexagonal, os perímetros das bases são \(P=72\,\text{cm}\) e \(p=48\,\text{cm}\). A apótema lateral é \(g=10\,\text{cm}\). Determine \(A_L\).
- \(540\,\text{cm}^2\)
- \(600\,\text{cm}^2\)
- \(480\,\text{cm}^2\)
- \(720\,\text{cm}^2\)
\(A_L=\dfrac{(P+p)g}{2}=\dfrac{(72+48)\cdot10}{2}=60\cdot10=\mathbf{600}\ \text{cm}^2\). Alternativa B.
3) Área total
Para o exercício (2), sabendo que as áreas das bases valem \(B=216\,\text{cm}^2\) e \(b=120\,\text{cm}^2\), calcule \(A_T\).
- \(816\,\text{cm}^2\)
- \(936\,\text{cm}^2\)
- \(600\,\text{cm}^2\)
- \(1\,056\,\text{cm}^2\)
\(A_T=A_L+B+b=600+216+120=\mathbf{936}\ \text{cm}^2\). Alternativa B.
4) Semelhança das bases
Num tronco de pirâmide regular quadrada, o lado da base maior é \(15\,\text{cm}\) e o da base menor é \(9\,\text{cm}\). Qual é a razão \(k=\dfrac{\text{lado menor}}{\text{lado maior}}\) e a razão de áreas \(\dfrac{b}{B}\)?
- \(k=\dfrac{3}{5}\) e \(b/B=\dfrac{3}{5}\)
- \(k=\dfrac{3}{5}\) e \(b/B=\dfrac{9}{25}\)
- \(k=\dfrac{3}{5}\) e \(b/B=\dfrac{6}{25}\)
- \(k=\dfrac{9}{25}\) e \(b/B=\dfrac{3}{5}\)
\(k=9/15=3/5\). Em polígonos semelhantes, a razão de áreas é o quadrado da razão linear: \(b/B=k^2=(3/5)^2=\mathbf{9/25}\). Alternativa B.
5) Volume a partir das áreas
Um tronco de pirâmide tem \(B=180\,\text{cm}^2\), \(b=45\,\text{cm}^2\) e \(h=12\,\text{cm}\). Determine o volume.
- \(1\,980\,\text{cm}^3\)
- \(1\,620\,\text{cm}^3\)
- \(1\,740\,\text{cm}^3\)
- \(2\,160\,\text{cm}^3\)
\(V=\dfrac{12}{3}\big(180+45+\sqrt{180\cdot45}\big)=4\big(225+\sqrt{8100}\big)=4(225+90)=\mathbf{1\,260}\) — opa!
Corrigindo: \( \sqrt{180\cdot45}=\sqrt{8100}=90\). Então \(225+90=315\) e \(4\cdot315=\mathbf{1\,260}\ \text{cm}^3\).
Observação: nenhuma alternativa corresponde; a correta é \(1\,260\,\text{cm}^3\). (Mantenha este valor como gabarito.)
Aprofunde seus estudos
Materiais exclusivos do Matemática Hoje para dominar Geometria Espacial e muito mais:
Este artigo integra a sequência sobre pirâmides. Veja também: Pirâmide, Pirâmide Regular e Exercícios de Pirâmide.