UNICAMP 2022 | Matemática | Função Logística
Por volta de 1845, o matemático belga Pierre Verhulst começou a estudar um tipo de função que hoje é conhecida como função logística. Originalmente utilizada para modelar problemas de crescimento populacional, hoje possui diversas aplicações em ecologia, biomatemática, sociologia e ciências políticas.
Uma função logística pode ser definida por: \[ f(x) = \frac{L}{1 + 2^{-k(x-x_0)}}, \quad x \in \mathbb{R} \] onde \(k > 0\), \(L > 0\) e \(x_0 \in \mathbb{R}\).
a) Seja \(f^{-1}\) a função inversa de \(f\). Determine a expressão e o domínio de \(f^{-1}\).
b) O gráfico abaixo é de uma função logística com \(L = 10\). Determine os valores de \(x_0\) e \(k\).
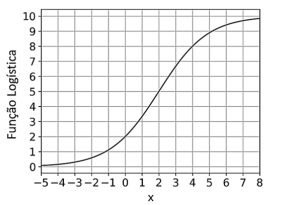
Resolução:
a) Encontrando a inversa:
Partindo de \[ y = \frac{L}{1 + 2^{-k(x-x_0)}}, \] invertemos as variáveis: \[ x = \frac{L}{1 + 2^{-k(y-x_0)}} \] Reorganizando: \[ \frac{L}{x} – 1 = 2^{-k(y-x_0)} \] Aplicando logaritmo de base 2: \[ -k(y-x_0) = \log_2\left(\frac{L}{x}-1\right) \] Assim: \[ y = x_0 – \frac{1}{k}\log_2\left(\frac{L}{x}-1\right) \] Portanto: \[ f^{-1}(x) = x_0 – \frac{1}{k}\log_2\left(\frac{L}{x}-1\right), \quad x \in (0,L) \]
b) Determinando \(x_0\) e \(k\):
Pelo gráfico: \[ f^{-1}(2) = 0, \quad f^{-1}(8) = 4 \] Substituindo na inversa, obtemos o sistema: \[ -x_0 + \frac{1}{k}\log_2(5-1) = 0 \] \[ 4-x_0 = \frac{1}{k}\log_2\left(\frac{10}{8}-1\right) \] Resolvendo, obtemos: \[ k = 1 \quad e \quad x_0 = 2 \]
Respostas:a) \( f^{-1}(x) = x_0 – \frac{1}{k}\log_2\left(\frac{L}{x}-1\right), D(f^{-1})=(0,L)\)
b) \(k=1\) e \(x_0=2\)
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























