UNICAMP 2022 | Matemática | Geometria Analítica e Áreas
Seja \( K \) a região poligonal, no plano cartesiano, dos pontos \((x, y)\) que satisfazem: \[ x \ge 0, \quad y \ge 0, \quad x + y \le 3, \quad 3x + y \le 5 \] A área hachurada na figura abaixo representa a região \( K \) no plano cartesiano.
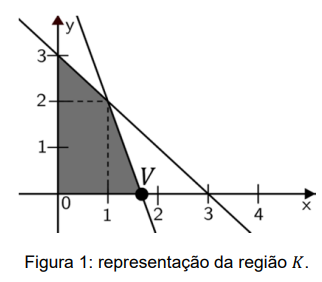
a) Determine as coordenadas do vértice \( V \), indicado na Figura 1, e a área da região \( K \).
b) Determine o maior valor de \( 2x + y \) para \((x, y) \in K\).
Resolução:
a) Encontrando o vértice \(V\):
O vértice \(V\) é a interseção das retas: \[ x + y = 3 \quad (r) \quad \text{e} \quad 3x + y = 5 \quad (s) \] Subtraindo as equações: \[ (3x + y) – (x + y) = 5 – 3 \implies 2x = 2 \implies x = 1 \] Substituindo em \(x + y = 3\): \[ 1 + y = 3 \implies y = 2 \] Logo, o vértice \(V\) é \( \left(\frac{5}{3},0 \right)\) pela projeção no eixo \(x\) da reta \(3x+y=5\) interceptando \(y=0\).
Cálculo da área \(S\):
A área de \(K\) é a soma do triângulo \(ABC\) e do trapézio \(ACOV\): \[ S = 1 \cdot 1/2 + \frac{5/3+1}{2} \cdot 2 = \frac{19}{6} \]
b) Determinando o valor máximo de \(2x+y\):
Considerando o feixe de retas \(y = -2x + p\), paralelo a \(2x+y=\text{constante}\), a maior interseção ocorre passando por \(A(1,2)\): \[ 2\cdot1 + 2 = 4 \]
Respostas:a) \( V = \left(\frac{5}{3}, 0 \right)\) e área \( \frac{19}{6} \)
b) \( 2x + y = 4 \)
