A poluição de rios, lagos e lagoas é um dos grandes problemas enfrentados pela sociedade moderna. Uma indústria despeja numa lagoa, de forma indevida, água contaminada por um poluente a uma certa taxa. Dependendo da vazão da lagoa e da concentração do poluente, é possível verificar que a quantidade total desse poluente na lagoa num tempo \( t \), denotada por \( Q(t) \), é dada por:
\[ Q(t) = 20 + 2 sen(t) – 4 \cos(t) \]
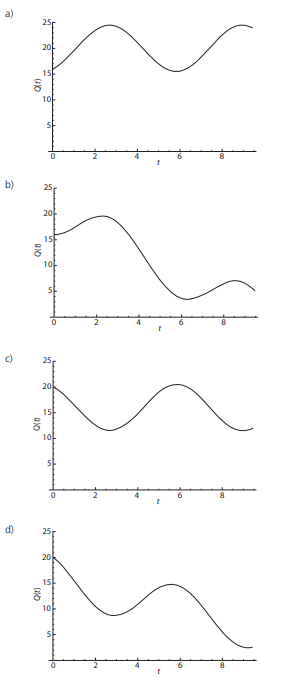
O gráfico que melhor representa \( Q(t) \) é:
1º Passo – Escrever a função na forma \( R sen(t – \alpha) + k \):
Determinando a amplitude: \[ R = \sqrt{2^2 + (-4)^2} = \sqrt{20} = 2\sqrt{5} \] Como \( sen \alpha = \frac{2}{2\sqrt{5}} = \frac{1}{\sqrt{5}} \) e \( \cos \alpha = \frac{2}{\sqrt{5}} \), obtemos: \[ Q(t) = 20 + 2\sqrt{5}\,sen(t – \alpha) \]
2º Passo – Intervalo de valores de \( Q(t) \):
\[ 20 – 2\sqrt{5} \le Q(t) \le 20 + 2\sqrt{5} \] Aproximadamente: \[ 15,52 \le Q(t) \le 24,48 \]
3º Passo – Conclusão sobre o gráfico correto:
O gráfico que inicia próximo de 16, atinge um pico próximo de 24 e oscila periodicamente é o **gráfico da alternativa A**.
Resposta Final: **Alternativa A**
Observação: Também seria possível resolver por exclusão calculando \( Q(0) \) e \( Q(\pi) \).
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























