Nesta questão da UNICAMP 2026, trabalhamos com Geometria Plana e Trigonometria dentro de um quadrado. A ideia é relacionar o ângulo no vértice, cujo cosseno é conhecido, com a posição dos pontos em um quadrado de lado x, para determinar a área do triângulo PMQ. É uma questão que mistura simetria, interpretação geométrica e uso de fórmulas trigonométricas.
🔗 Dando continuidade à sequência: Questão 49 – Análise Combinatória e Permutação com Restrição
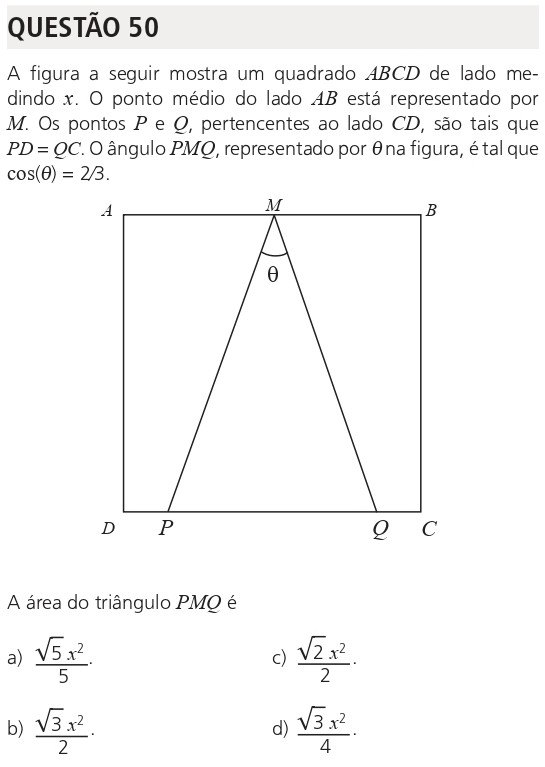
Descrição da imagem: quadrado ABCD com lado x, ponto médio M no topo e segmentos MP e MQ formando o ângulo θ.
✅ Clique aqui para ver a solução passo a passo
1) Sistema de coordenadas e simetria
Vamos colocar o quadrado em um plano cartesiano:
D = (0, 0), C = (x, 0), B = (x, x), A = (0, x).
O ponto M é o ponto médio de AB, logo:
M = (x/2, x)
Os pontos P e Q pertencem ao lado CD, isto é, sobre o segmento de (0, 0) até (x, 0).
Seja P = (p, 0) e Q = (q, 0).
A condição PD = QC implica:
PD = p e QC = x − q
p = x − q ⟹ q = x − p
Isso mostra que P e Q são simétricos em relação ao ponto médio da base, ou seja, em relação à reta vertical que passa por M.
2) Vetores MP e MQ
Seja:
d = p − x/2 (deslocamento horizontal de P em relação a M)
Então:
P = (x/2 + d, 0) ⟹ MP = (d, −x)
Q = (x/2 − d, 0) ⟹ MQ = (−d, −x)
O ângulo θ é o ângulo entre os vetores MP e MQ.
3) Cálculo de cos(θ)
Produto escalar:
MP · MQ = d·(−d) + (−x)·(−x) = −d² + x²
Módulos:
|MP|² = d² + x²
|MQ|² = d² + x²
|MP| = |MQ| = √(d² + x²)
Assim:
cos(θ) = (MP · MQ) / (|MP|·|MQ|)
= (x² − d²) / (x² + d²)
A questão informa que:
cos(θ) = 2/3
Logo:
(x² − d²) / (x² + d²) = 2/3
4) Encontrando d em função de x
3(x² − d²) = 2(x² + d²)
3x² − 3d² = 2x² + 2d²
x² = 5d²
d² = x² / 5
5) Comprimento da base PQ
Os pontos P e Q estão simétricos em relação a x/2, logo:
PQ = 2|d| = 2·(x/√5) = 2x/√5
6) Altura do triângulo PMQ
A base PQ está sobre o lado CD (eixo y = 0).
O ponto M tem coordenadas (x/2, x), então a distância vertical de M à base é:
x
7) Área do triângulo PMQ
A área é:
A = (base · altura) / 2
A = (PQ · x) / 2
A = ( (2x/√5) · x ) / 2
A = x² / √5
Racionalizando o denominador:
A = x² / √5 · (√5/√5) = (√5 x²) / 5
✅ Resposta correta: alternativa A = (√5 x²) / 5













