Valor máximo e mínimo de uma função

Neste guia você aprende a localizar valor máximo e valor mínimo (também chamados de absolutos ou globais) e a distinguir de máximos/mínimos locais. Para revisão rápida: Gráfico de uma Função, Funções Crescente/Decrescente/Constante, Domínio e Zeros.

Exemplo visual de máximo e mínimo da função g(x) com destaques no gráfico

Notação usada

\( \mathbb{R} \) (reais), \( \infty \) (infinito), \( x\in D \) (x pertence ao domínio \(D\)), \( [a,b] \) intervalo fechado, \( (a,b) \) aberto, \( \le, \ge \) (menor/maior ou igual), \( \operatorname{argmax} \) e \( \operatorname{argmin} \) (pontos onde ocorrem máximo e mínimo).

Definições precisas (com símbolos)

Máximo e mínimo absolutos em \(D\) \[ \text{Máximo: } M=\max_{x\in D} f(x) \iff \big(f(x)\le M,\ \forall x\in D\big)\ \text{ e }\ \exists x_0\in D:\ f(x_0)=M. \] \[ \text{Mínimo: } m=\min_{x\in D} f(x) \iff \big(f(x)\ge m,\ \forall x\in D\big)\ \text{ e }\ \exists x_1\in D:\ f(x_1)=m. \]

Máximo/Mínimo local em \(x_0\) \[ \exists\,\delta>0:\ f(x)\le f(x_0)\ (\text{ou }\ge)\ \ \forall x\in (x_0-\delta,\ x_0+\delta)\cap D. \]

Teorema do Valor Extremo: se \(f\) é contínua em \([a,b]\), então \(f\) atinge um máximo e um mínimo em \([a,b]\).

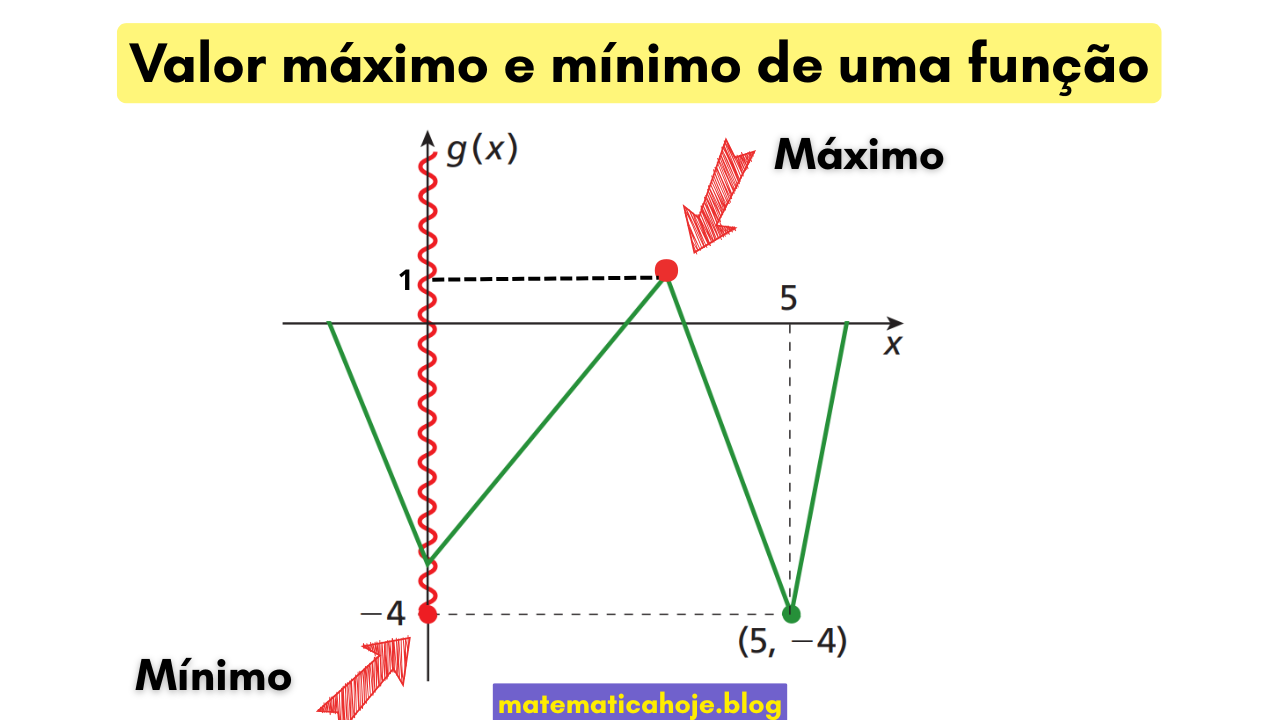
Como identificar no gráfico

Os “picos” são candidatos a máximos locais; os “vales”, a mínimos locais.
Compare: extremos locais, quinas, pontos de troca de regra (funções por partes) e as extremidades do intervalo.
O ponto precisa pertencer ao domínio: marcação vazada (ponto excluído) não pode ser máximo/mínimo absoluto.

Como decidir pela expressão

Equações simples: para \( y=mx+b \) não há extremos; para \( ax^2+bx+c \), \[ x_v=-\frac{b}{2a},\qquad \begin{cases} a>0 \Rightarrow \text{mínimo em }x_v,\\[2pt] a<0 \Rightarrow \text{máximo em }x_v. \end{cases} \]
Com derivadas: pontos críticos \( f'(x)=0 \) ou onde \( f’ \) não existe.
- \(1^\circ\) teste: \(f’\) muda de \(+\) para \(-\) \(\Rightarrow\) máximo; de \(-\) para \(+\) \(\Rightarrow\) mínimo.
- \(2^\circ\) teste: \(f”(x_0)>0\Rightarrow\) mínimo; \(f”(x_0)<0\Rightarrow\) máximo (quando aplicável).
Em \([a,b]\): avalie candidatos + \(f(a)\) e \(f(b)\) e compare os valores.

📘 Precisa do “cola-resumo” com vértice, testes e símbolos? Veja o eBook Fórmulas Matemática.

Exemplos resolvidos

1) Quadrática com máximo

\( f(x)=-x^2+4x+1 \) (\(D=\mathbb{R}\)). Vértice: \( x_v=-\dfrac{4}{2\cdot(-1)}=2 \). Valor \( f(2)=-4+8+1=5 \Rightarrow \) máximo absoluto \(=5\). Sem mínimo absoluto em \( \mathbb{R} \) ( \( f(x)\to-\infty \) ).

2) Quadrática com mínimo

\( g(x)=x^2-6x+5 \). \( x_v=\dfrac{6}{2}=3 \). \( g(3)=9-18+5=-4 \Rightarrow \) mínimo absoluto \(=-4\). Sem máximo absoluto em \( \mathbb{R} \).

3) Valor absoluto

\( h(x)=|x-2|+1 \). Vértice em \(x=2\) com \(h(2)=1\Rightarrow\) mínimo \(=1\). Sem máximo em \( \mathbb{R} \).

4) Intervalo fechado

\( p(x)=x^3-3x^2+1 \) em \([0,3]\). \( p'(x)=3x^2-6x=3x(x-2) \Rightarrow x=0,2 \). \[ p(0)=1,\quad p(2)=8-12+1=-3,\quad p(3)=27-27+1=1. \] Máximo \(=1\) (em \(x=0\) e \(x=3\)); mínimo \(=-3\) (em \(x=2\)).

5) Intervalo aberto

\( q(x)=\dfrac{1}{x} \) em \( (0,1) \). É decrescente, não atinge máximo; \( \inf q = 1 \) mas não é alcançado porque \(1\notin(0,1)\).

Quadro-resumo

Checklist para máximos e mínimos
O que verificar	Como fazer	Observações
Domínio e tipo de intervalo	\([a,b]\) fechado ou \((a,b)\) aberto? Há pontos excluídos?	Contínua em \([a,b]\) \(\Rightarrow\) extremos existem (TVE).
Pontos críticos	Resolver \(f'(x)=0\) e onde \(f’\) não existe	Candidatos a extremos locais.
Extremidades	Calcular \(f(a)\) e \(f(b)\) (se \(a,b\in D\))	Podem fornecer extremos absolutos.
Comparação final	Comparar todos os valores \(f(x)\)	Maior \(\Rightarrow\) máximo; menor \(\Rightarrow\) mínimo.
Casos especiais	Plateaus, buracos, assíntotas	Máximo pode não existir; atenção ao domínio.