Vértice da parábola

Vértice da parábola: fórmulas, passo a passo e exemplos

Vértice da parábola: como encontrar e interpretar

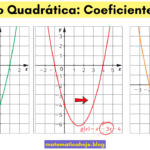
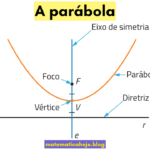
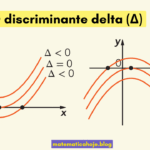
O vértice de \(f(x)=ax^2+bx+c\) é o ponto mais alto (máximo) quando \(a<0\) ou o mais baixo (mínimo) quando \(a>0\). Ele concentra a informação de valor máximo/mínimo, forma do gráfico e do eixo de simetria.

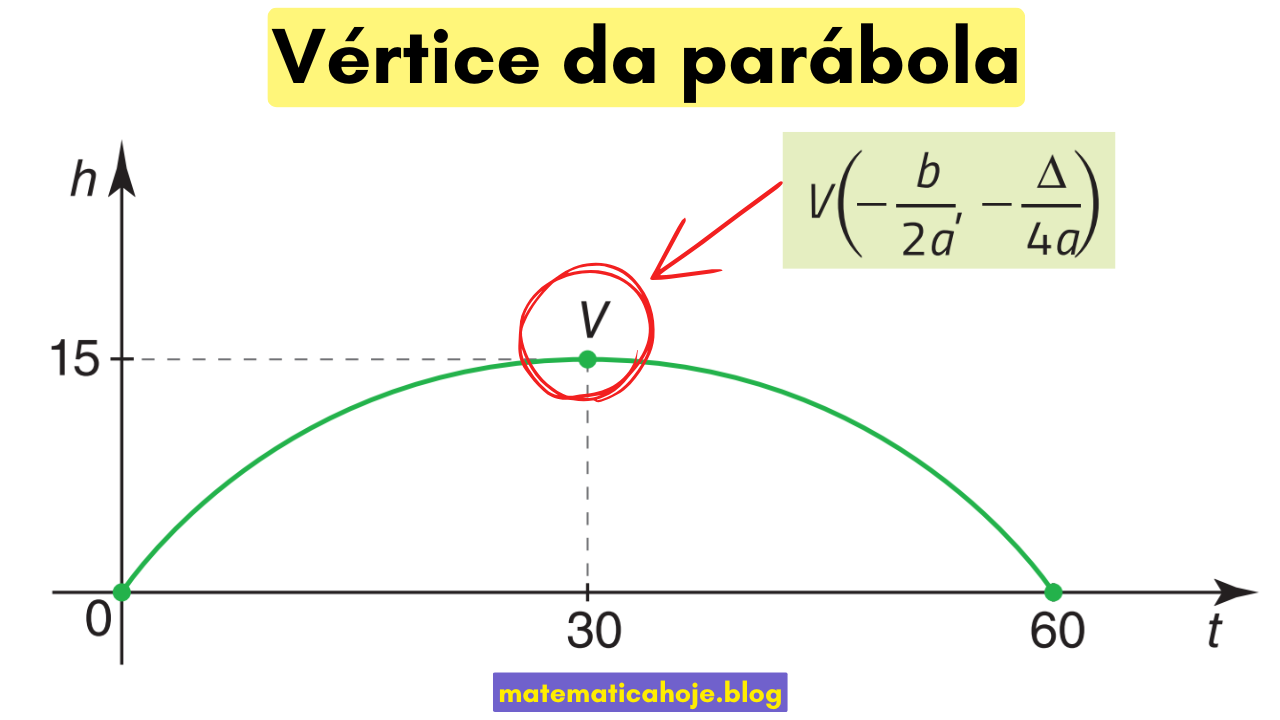
Fórmulas essenciais

\[ x_v=-\frac{b}{2a},\qquad y_v=-\frac{\Delta}{4a}\quad \text{com}\ \Delta=b^2-4ac. \]

Equivalente via forma canônica: \(f(x)=a(x-h)^2+k\Rightarrow V=(h,k)\).

Como calcular (3 passos)

Leia \(a,b,c\).
Calcule \(x_v=-\dfrac{b}{2a}\).
Calcule \(y_v\) por \(y_v=f(x_v)\) ou \(y_v=-\dfrac{\Delta}{4a}\).

Interpretação

O eixo de simetria é \(x=x_v\).
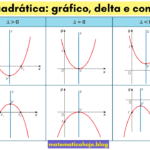
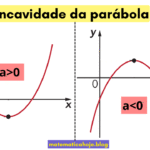
\(a>0\) ⟶ vértice é mínimo; \(a<0\) ⟶ vértice é máximo.
Em contexto físico (lançamentos), \(x_v\) é o instante de pico e \(y_v\) a altura máxima.

Gráfico destacando o vértice V de uma parábola e as fórmulas xv = -b/(2a) e yv = -Δ/(4a).

📘 E-book de Fórmulas de Matemática

Todas as fórmulas de quadrática (vértice, Δ, raízes, canônica) organizadas para revisão rápida. Excelente para provas e ENEM.

Quero o E-book de Fórmulas

Exemplos resolvidos (contas em coluna)

Exemplo 1 — Vértice de \(f(x)=-x^2+6x+5\)

\[ \begin{aligned} a&=-1,\ b=6,\ c=5\\[2pt] x_v&=-\frac{b}{2a}\\ &=-\frac{6}{2(-1)}\\ &=-\frac{6}{-2}\\ &=3\\[6pt] y_v&=f(3)\\ &=-\,(3)^2+6\cdot 3+5\\ &=-9+18+5\\ &=14 \end{aligned} \]

Como \(a<0\), \(V=(3,14)\) é um máximo.

Exemplo 2 — Vértice de \(g(x)=2x^2-8x+1\)

\[ \begin{aligned} a&=2,\ b=-8,\ c=1\\[2pt] x_v&=-\frac{-8}{2\cdot 2}\\ &=\frac{8}{4}\\ &=2\\[6pt] y_v&=g(2)\\ &=2\cdot (2)^2-8\cdot 2+1\\ &=2\cdot 4-16+1\\ &=8-16+1\\ &=-7 \end{aligned} \]

Como \(a>0\), \(V=(2,-7)\) é um mínimo.

Exemplo 3 — Forma canônica e vértice de \(h(x)=3x^2+12x-7\)

\[ \begin{aligned} h(x)&=3\left[x^2+4x\right]-7\\ &=3\left[(x+2)^2-4\right]-7\\ &=3(x+2)^2-12-7\\ &=3(x+2)^2-19 \end{aligned} \]

Logo \(V=(-2,-19)\) (mínimo).

Exemplo 4 — Pico de um lançamento: \(H(t)=-0.4t^2+12t\)

\[ \begin{aligned} a&=-0.4,\ b=12\\[2pt] t_{\text{pico}}&=-\frac{b}{2a}\\ &=-\frac{12}{2(-0.4)}\\ &=-\frac{12}{-0.8}\\ &=15\\[6pt] H(15)&=-0.4(15)^2+12(15)\\ &=-0.4\cdot 225+180\\ &=-90+180\\ &=90 \end{aligned} \]

Altura máxima \(90\) (unidades do gráfico) ocorre em \(t=15\).

Erros comuns

Usar \(c\) como ordenada do vértice. Cuidado: \(c=f(0)\), enquanto \(y_v=-\dfrac{\Delta}{4a}\).
Esquecer o sinal de \(a\) ao interpretar se o vértice é máximo ou mínimo.
Confundir “deslocamento horizontal” com o efeito de \(b\): o eixo é \(x=-\dfrac{b}{2a}\).

Exercícios propostos

1) Encontre o vértice de \(p(x)=-2x^2+10x-1\).

Gabarito

\[ \begin{aligned} a&=-2,\ b=10,\ c=-1\\ x_v&=-\frac{10}{2(-2)}=2.5\\ y_v&=p(2.5)\\ &=-2(2.5)^2+10(2.5)-1\\ &=-2\cdot 6.25+25-1\\ &=-12.5+24\\ &=11.5 \end{aligned} \]

Vértice \(V=(2{,}5,\,11{,}5)\) — máximo.

2) Transforme \(q(x)=x^2-4x+13\) em canônica e leia \(V\).

Gabarito

\[ \begin{aligned} q(x)&=(x^2-4x)+13\\ &=(x-2)^2-4+13\\ &=(x-2)^2+9 \end{aligned} \]

\(V=(2,9)\) — mínimo.

3) Para \(r(x)=5x^2+bx+20\), determine \(b\) tal que \(x_v=1\).

Gabarito

\[ \begin{aligned} x_v&=-\frac{b}{2a}=1\\ -\frac{b}{2\cdot 5}&=1\\ -\frac{b}{10}&=1\\ b&=-10 \end{aligned} \]

Continue por aqui (links internos)

Função Quadrática (guia completo) Gráfico da função quadrática Valor máximo e mínimo Coeficiente \(a\) Coeficientes \(b\) e \(c\) Pontos notáveis da parábola Foco e diretriz

Materiais recomendados (produtos do blog)

Mapas Mentais de Matemática Preparação ENEM Matemática Coleção com 10 E-books Banco de Questões de Matemática E-book de Fórmulas (referência rápida)

Relacionadas

Estudo do sinal da Função Quadrática

Forma fatorada da Função Quadrática

Função Quadrática: Coeficientes b e c

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.