📍 Vértice da parábola
O vértice V da parábola de uma função quadrática é um ponto do gráfico no qual identificamos uma mudança de comportamento: de crescente para decrescente ou, ao contrário, de decrescente para crescente.
Seja \( V(x_v, y_v) \) o vértice da parábola da função quadrática \( f: \mathbb{R} \rightarrow \mathbb{R} \), se \( a > 0 \), ela é crescente no intervalo \( ]- \infty, x_v] \), e decrescente em \( [x_v, +\infty[ \), e se \( a < 0 \), ela é decrescente em \( ]- \infty, x_v] \), e crescente em \( [x_v, +\infty[ \).
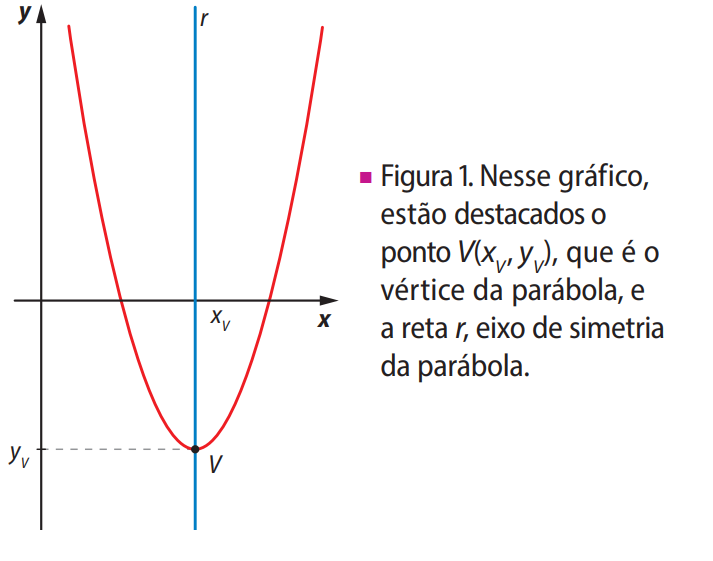
O eixo de simetria da parábola de uma função quadrática é a reta perpendicular ao eixo \( x \), que passa pelo vértice \( V \).
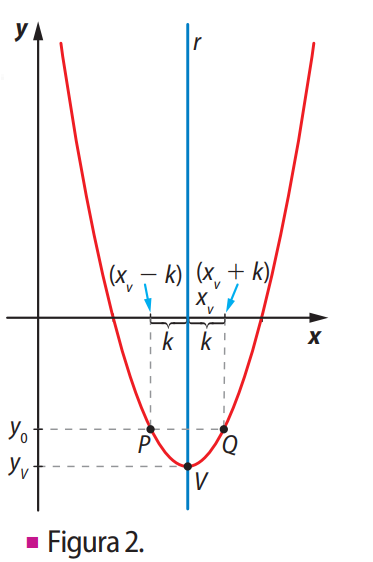
Podemos obter as coordenadas do vértice de uma parábola a partir da equação geral \( f(x) = ax^2 + bx + c \). Sabendo que o eixo de simetria divide a parábola ao meio, os zeros da função (quando existentes) estão à mesma distância desse eixo.
Vamos calcular a abscissa do vértice:
Agora, substituímos esse valor na função para encontrar a ordenada do vértice:
Desenvolvendo:
Portanto, as coordenadas do vértice da parábola são:
💡 Saiba que: Facilitar o esboço do gráfico de uma função quadrática depende de identificar corretamente o vértice, os zeros da função e a concavidade da parábola.
Questão 1. Determine as coordenadas do vértice da função quadrática \( f(x) = 2x^2 – 8x + 3 \).
🔎 Ver solução
Para encontrar as coordenadas do vértice da parábola, usamos:
\( x_v = \frac{-b}{2a} \), com \( a = 2 \) e \( b = -8 \):
\( x_v = \frac{-(-8)}{2 \cdot 2} = \frac{8}{4} = 2 \)
Agora, substituímos \( x = 2 \) na função:
\( y_v = f(2) = 2(2)^2 – 8(2) + 3 = 8 – 16 + 3 = -5 \)
Portanto, o vértice da parábola é:
\( V = (2, -5) \)
Questão 2. Uma empresa calcula o lucro \( L(x) = -3x^2 + 12x + 20 \), em milhares de reais, em função da quantidade de unidades produzidas \( x \). Qual é o número de unidades que maximiza o lucro e qual é esse lucro máximo?
🔎 Ver solução
A função do lucro é uma parábola voltada para baixo, pois \( a = -3 \). O valor máximo ocorre no vértice.
Calculamos:
\( x_v = \frac{-b}{2a} = \frac{-12}{2 \cdot (-3)} = \frac{-12}{-6} = 2 \)
Substituindo \( x = 2 \) na função:
\( L(2) = -3(2)^2 + 12(2) + 20 = -12 + 24 + 20 = 32 \)
Assim, o lucro máximo é de R$ 32.000,00, quando são produzidas 2 mil unidades.
Resposta: O lucro é máximo com 2 mil unidades, e o valor máximo é R$ 32.000,00.
Questão 3. Um projétil é lançado verticalmente e sua altura em função do tempo (em segundos) é dada por \( h(t) = -5t^2 + 20t \), com \( h \) em metros. Qual a altura máxima atingida?
🔎 Ver solução
A equação da altura é uma função quadrática com \( a = -5 \) e \( b = 20 \).
O tempo em que a altura é máxima é dado por:
\( t_v = \frac{-b}{2a} = \frac{-20}{2 \cdot (-5)} = \frac{-20}{-10} = 2 \)
Substituímos \( t = 2 \) na função:
\( h(2) = -5(2)^2 + 20(2) = -20 + 40 = 20 \)
Resposta: A altura máxima atingida pelo projétil é de 20 metros.
Questão 4. Uma função quadrática tem zeros em \( x = -1 \) e \( x = 5 \), e passa pelo ponto \( (2, -9) \). Determine sua lei de formação na forma \( f(x) = ax^2 + bx + c \).
🔎 Ver solução
Sabemos que os zeros são \( x_1 = -1 \) e \( x_2 = 5 \), então a forma fatorada é:
\( f(x) = a(x + 1)(x – 5) \)
Usamos o ponto \( (2, -9) \) para encontrar \( a \):
\( -9 = a(2 + 1)(2 – 5) \Rightarrow -9 = a(3)(-3) \Rightarrow -9 = -9a \Rightarrow a = 1 \)
Logo:
\( f(x) = (x + 1)(x – 5) \Rightarrow f(x) = x^2 – 4x – 5 \)
Resposta: A função é \( f(x) = x^2 – 4x – 5 \).













