Volume do Paralelepípedo — fórmula geral, conversões e exercícios
Tudo o que você precisa para calcular o volume do paralelepípedo: fórmula geral \(V=A_{\text{base}}\cdot h\), caso retângulo \(V=a\cdot b\cdot c\), conversão para litros, exemplos com contas na vertical e exercícios com gabarito.
1) O que é e quando usar cada fórmula
Paralelepípedo é um prisma cujas faces opostas são paralelogramos. No dia a dia, trabalhamos muito com o paralelepípedo retângulo (todas as faces são retângulos). O volume mede o espaço interno do sólido.
2) Fórmulas do volume
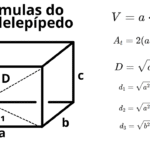
Fórmula geral (reto e oblíquo)
\(V = A_{\text{base}}\cdot h\), onde \(h\) é a altura perpendicular ao plano da base.
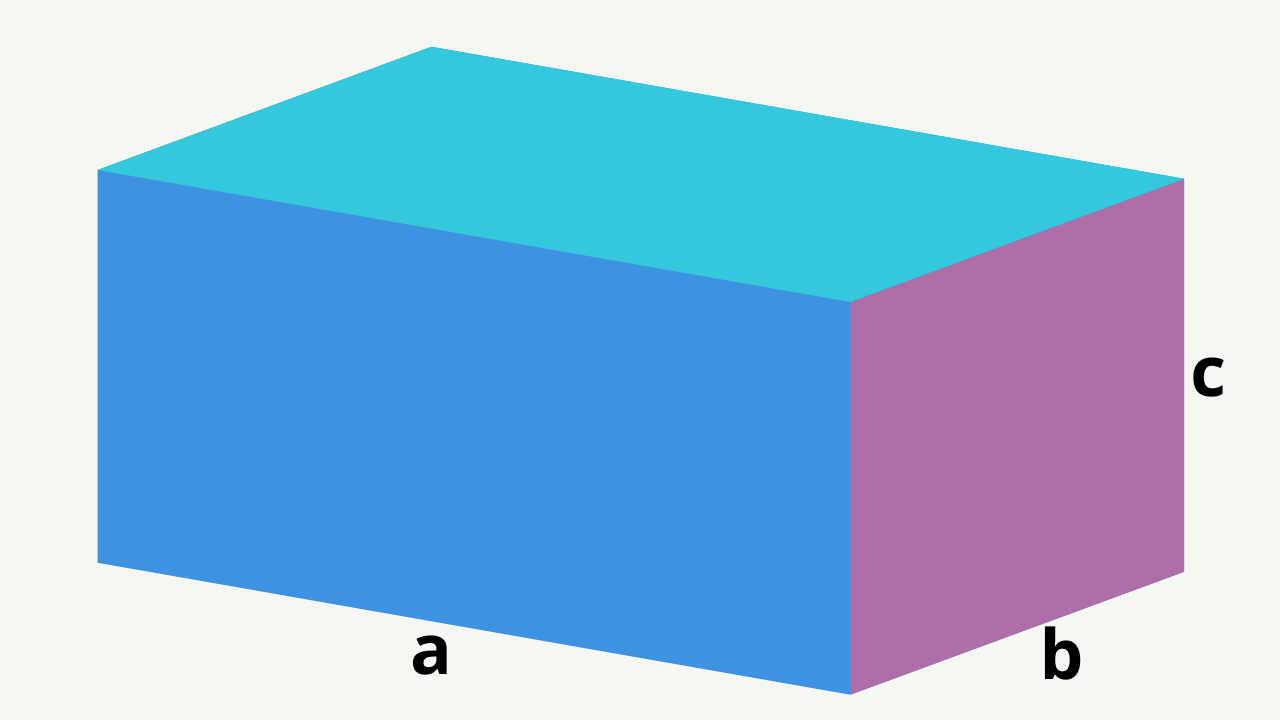
Caso retângulo (arestas ortogonais)
\(V = a\cdot b\cdot c\)
Multiplique comprimento, largura e altura (mesma unidade).
Conversões úteis
- \(1\ \text{dm}^3 = 1\ \text{L}\)
- \(1\ \text{m}^3 = 1000\ \text{L}\)
- \(1\ \text{L} = 1000\ \text{cm}^3\)
3) Exemplos resolvidos (contas na vertical)
-
Enunciado. Um paralelepípedo retângulo tem \(a=12\ \text{cm}\), \(b=8\ \text{cm}\) e \(c=5\ \text{cm}\). Calcule o volume.
Ver solução
$$\begin{aligned} V&=a\cdot b\cdot c\\ &=12\cdot8\cdot5\\ &=96\cdot5\\ &=\mathbf{480\ \text{cm}^3} \end{aligned}$$ -
Enunciado. Uma caixa tem base \(30\ \text{cm}\times 25\ \text{cm}\) e altura \(0{,}4\ \text{m}\). Quantos litros cabem?
Ver solução
$$\begin{aligned} 0{,}4\ \text{m}&=40\ \text{cm}\\[2pt] V&=30\cdot25\cdot40\\ &=750\cdot40\\ &=30\,000\ \text{cm}^3\\ &=\mathbf{30\ \text{L}}\quad(1000\ \text{cm}^3=1\ \text{L}) \end{aligned}$$ -
Enunciado. Um paralelepípedo oblíquo tem base paralelogramo de área \(A_{\text{base}}=72\ \text{cm}^2\) e altura perpendicular \(h=9\ \text{cm}\). Ache \(V\).
Ver solução
$$\begin{aligned} V&=A_{\text{base}}\cdot h\\ &=72\cdot9\\ &=\mathbf{648\ \text{cm}^3} \end{aligned}$$ -
Enunciado. O volume de um paralelepípedo retângulo é \(V=2{,}16\ \text{m}^3\). Sabendo \(a=1{,}2\ \text{m}\) e \(b=0{,}9\ \text{m}\), encontre \(c\).
Ver solução
$$\begin{aligned} V&=a\cdot b\cdot c\\ 2{,}16&=1{,}2\cdot0{,}9\cdot c\\ 2{,}16&=1{,}08\cdot c\\ c&=\dfrac{2{,}16}{1{,}08}\\ c&=\mathbf{2{,}0\ \text{m}} \end{aligned}$$ -
Enunciado. Uma caixa d’água retangular deve armazenar \(1{,}5\ \text{m}^3\). Se a base é \(1{,}25\ \text{m}\times 0{,}8\ \text{m}\), qual a altura?
Ver solução
$$\begin{aligned} V&=a\cdot b\cdot c\\ 1{,}5&=1{,}25\cdot0{,}8\cdot c\\ 1{,}5&=1{,}0\cdot c\\ c&=\mathbf{1{,}5\ \text{m}} \end{aligned}$$
Erros comuns e dicas rápidas
- Unidades: padronize (cm com cm, m com m) antes de multiplicar.
- Oblíquo: use a altura perpendicular \(h\), não a aresta inclinada.
- Litros: calcule o volume em \( \text{cm}^3 \) ou \( \text{m}^3 \) e só então converta.
4) Questões (múltipla escolha, com solução em abre/fecha)
-
O volume de um paralelepípedo retângulo com dimensões \(a,b,c\) é:
- A) \(ab+ac+bc\)
- B) \(2(ab+ac+bc)\)
- C) \(a\cdot b\cdot c\)
- D) \(\sqrt{a^2+b^2+c^2}\)
Ver solução
Gabarito: C. $$\begin{aligned} V&=a\cdot b\cdot c \end{aligned}$$ -
Em um paralelepípedo oblíquo, o volume é calculado por:
- A) \(V=ab\cdot c\)
- B) \(V=A_{\text{base}}\cdot h\)
- C) \(V=\dfrac{A_{\text{base}}}{h}\)
- D) \(V=2(A_{\text{base}}+h)\)
Ver solução
Gabarito: B. $$\begin{aligned} V&=A_{\text{base}}\cdot h \end{aligned}$$ -
Uma caixa \(40\ \text{cm}\times 25\ \text{cm}\times 30\ \text{cm}\) tem volume (em litros):
- A) 2,5 L
- B) 25 L
- C) 300 L
- D) 30 L
Ver solução
Gabarito: D. $$\begin{aligned} V&=40\cdot25\cdot30\\ &=30\,000\ \text{cm}^3\\ &=\mathbf{30\ \text{L}} \end{aligned}$$ -
Se \(V=864\ \text{cm}^3\) e \(a=12\ \text{cm}\), \(b=6\ \text{cm}\), então \(c\) vale:
- A) \(8\ \text{cm}\)
- B) \(10\ \text{cm}\)
- C) \(12\ \text{cm}\)
- D) \(6\ \text{cm}\)
Ver solução
Gabarito: C. $$\begin{aligned} V&=a\cdot b\cdot c\\ 864&=12\cdot6\cdot c\\ 864&=72\cdot c\\ c&=\dfrac{864}{72}\\ c&=\mathbf{12\ \text{cm}} \end{aligned}$$
5) Perguntas frequentes
| Qual fórmula usar: \(a\cdot b\cdot c\) ou \(A_{\text{base}}\cdot h\)? | Use \(a\cdot b\cdot c\) no retângulo (arestas perpendiculares). No oblíquo, use \(V=A_{\text{base}}\cdot h\). |
|---|---|
| Como converter m³ em litros? | Multiplique por 1000. Ex.: \(2{,}5\ \text{m}^3=2500\ \text{L}\). |
| Preciso converter as unidades antes? | Sim. As três dimensões devem estar na mesma unidade para multiplicar. |