Zero da Função Afim (raiz / intercepto-x)
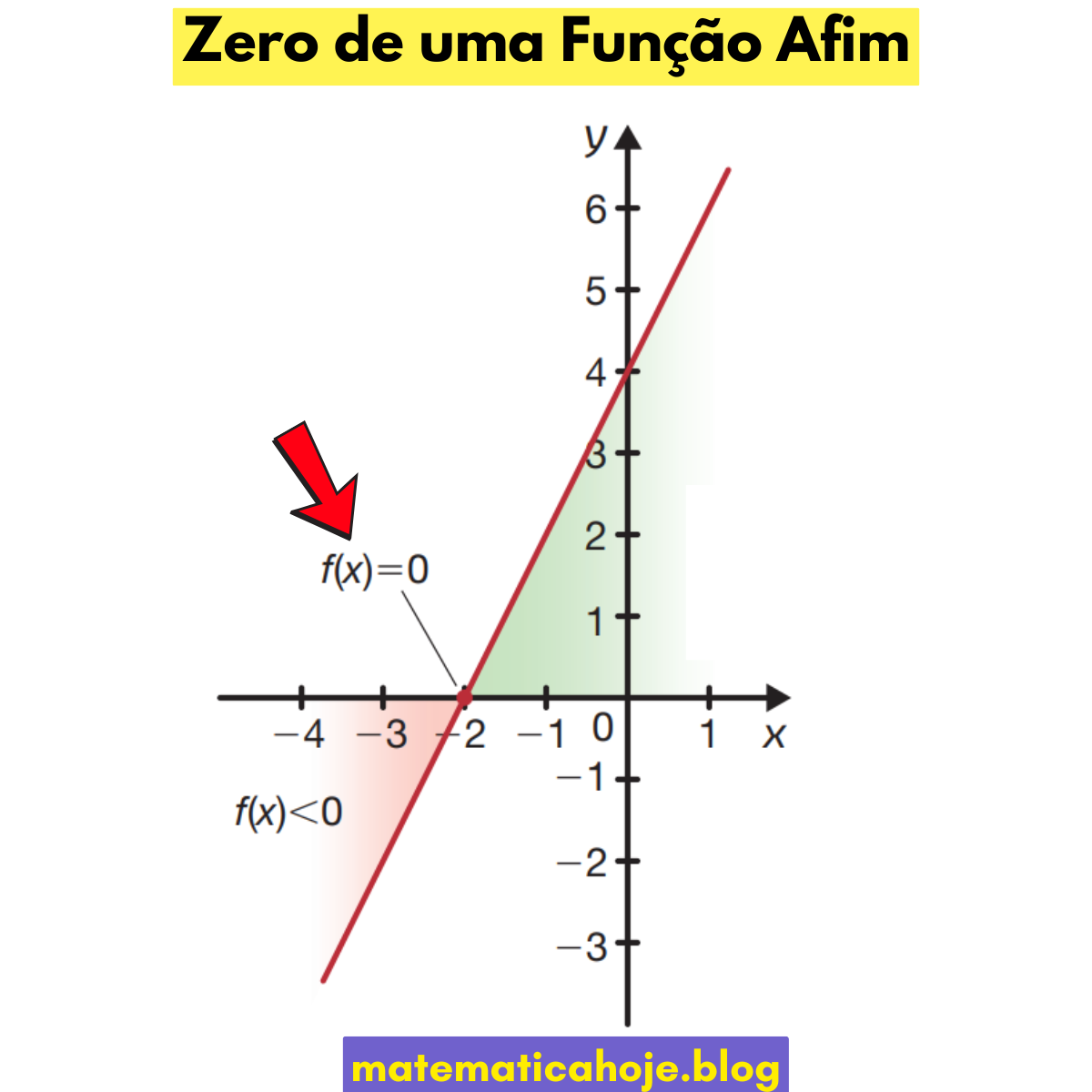
O zero da função afim — também chamado de raiz ou intercepto-x — é o valor de \(x\) onde a função assume zero: \(f(x)=0\). No gráfico, é o ponto em que a reta cruza o eixo \(x\). Conteúdo recorrente no ENEM Matemática e em bancos de questões.
Fórmula do zero da função afim
- Se \(a=0\) e \(b\neq 0\): função constante \(\Rightarrow\) não tem zero.
- Se \(a=0\) e \(b=0\): função nula \(\Rightarrow\) infinitos zeros (reta coincide com o eixo \(x\)).
Passo a passo (método da equação)
- Comece com \(f(x)=ax+b\).
- Resolva \(ax+b=0\).
- Obtenha \(x_0=-\dfrac{b}{a}\) (com \(a\neq 0\)).
Interpretação geométrica
\(x_0\) é a abscissa do ponto onde a reta corta o eixo \(x\). Para traçar a reta rapidamente, combine esse ponto com o intercepto em \(y\): \(B=(0,b)\). Veja o tutorial completo de gráfico aqui: como construir o gráfico da função afim.
📘 Fórmula sempre à mão
Reforce as fórmulas de função afim, linear e constante no eBook Fórmulas Matemática.
Baixar eBook de FórmulasExemplos resolvidos
Exemplo 1 — Lei explícita. Encontre o zero de \(f(x)=3x-9\) e interprete no gráfico.
Ver solução
\(x_0=-\dfrac{-9}{3}=3\). A reta cruza o eixo \(x\) em \(x=3\). Outro ponto fácil é \(B=(0,-9)\).
Exemplo 2 — A partir de dois pontos. A reta passa por \(A(1,2)\) e \(B(5,10)\). Determine o zero.
Ver solução
Inclinação \(a=\dfrac{10-2}{5-1}=\dfrac{8}{4}=2\). Ache \(b\) usando \(A\): \(2=2\cdot1+b \Rightarrow b=0\).
Logo \(f(x)=2x\). Zero em \(x_0=-\dfrac{0}{2}=0\) (passa pela origem).
Exemplo 3 — Palavra-problema. O lucro de uma lanchonete é \(L(q)=1{,}80q-270\), onde \(q\) é o número de unidades vendidas. Quantas unidades precisam ser vendidas para sair do prejuízo?
Ver solução
Marque o ponto de equilíbrio pelo zero: \(x_0=-\dfrac{-270}{1{,}80}=150\) unidades.
Erros comuns
- Esquecer o sinal em \(-\dfrac{b}{a}\) (troca de sinal do \(b\)).
- Dividir por \(a=0\): nesses casos, não há zero (a menos que \(b=0\)).
- Confundir zero (intercepto-x) com intercepto em \(y\) (ponto \(B=(0,b)\)).
Exercícios (com gabarito no abre/fecha)
1) Calcule o zero de \(g(x)=-2x+5\) e indique o ponto no eixo \(x\).
Ver solução
\(x_0=-\dfrac{5}{-2}=\dfrac{5}{2}=2{,}5\). Ponto \((2{,}5,0)\).
2) A reta com inclinação \(a=-\dfrac{3}{4}\) tem intercepto em \(y\) igual a \(b=6\). Determine o zero.
Ver solução
\(x_0=-\dfrac{6}{-3/4}=\dfrac{6}{3/4}=8\).
3) A função \(h(x)=k\) (constante) possui zero? Analise para \(k=0\) e \(k\neq 0\).
Ver solução
Se \(k=0\): infinitos zeros (reta sobre o eixo \(x\)). Se \(k\neq 0\): não possui zero.
4) A reta que passa por \(P(-1,3)\) e \(Q(2,-6)\) é afim. Encontre \(x_0\).
Ver solução
\(a=\dfrac{-6-3}{2-(-1)}=\dfrac{-9}{3}=-3\). Use \(P\): \(3=-3(-1)+b\Rightarrow b=0\). Logo \(f(x)=-3x\) ⇒ \(x_0=0\).
5) Determine o zero de \(p(x)=1{,}2x-0{,}84\) e arredonde às centésimas.
Ver solução
\(x_0=-\dfrac{-0{,}84}{1{,}2}=0{,}7\) ⇒ \(x_0=0,70\).
Continue estudando Função Afim
- Como construir o gráfico da função afim
- Taxa de variação da função afim (Δy/Δx)
- Interseção de retas (ponto comum)
- Função linear (b=0) • Função constante (a=0)