Zero de uma Função (ou Raiz)
Definição, técnicas para encontrar e exercícios resolvidos.
O zero (ou raiz) de uma função é o valor de entrada que zera a saída. Graficamente, são os pontos de interseção com o eixo \(x\). Dominar esse conceito ajuda em função quadrática, inequações, gráficos e problemas de ENEM/concursos.
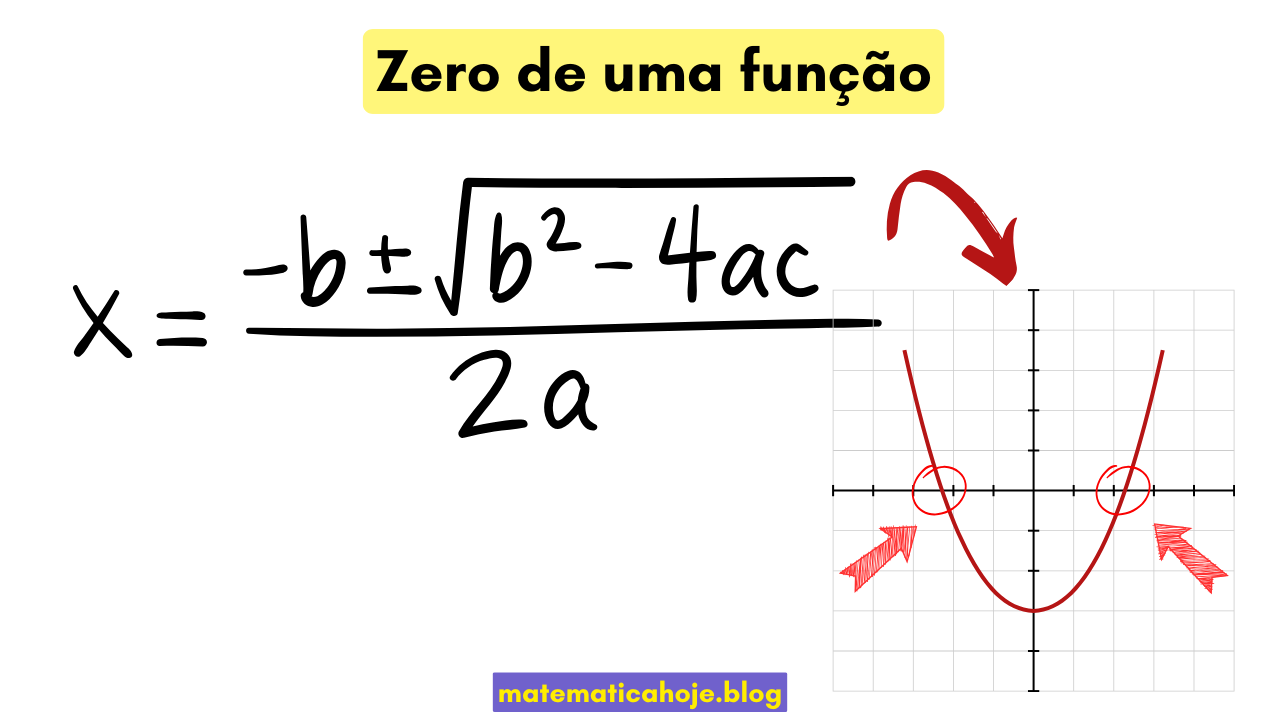
Ideias-chave
- Para achar zeros, resolva a equação \(f(x)=0\).
- Respeite o domínio: soluções fora dele devem ser descartadas.
- Uma função pode ter nenhum, um ou vários zeros reais.
Leituras relacionadas
Imagem de uma Função • Função do 2º Grau • Equações do 1º Grau • Logaritmos
Métodos rápidos por tipo de função
| Tipo | Como resolver \(f(x)=0\) | Observações |
|---|---|---|
| Afim \(ax+b\) | \(ax+b=0 \Rightarrow x=-\dfrac{b}{a}\) | \(a\ne0\) |
| Quadrática \(ax^2+bx+c\) | Bhaskara / completar quadrado | Discriminante \(\Delta=b^2-4ac\) |
| Polinômios | Fatorar: \(P(x)=k\prod(x-r_i)\) | Zeros são os \(r_i\) |
| Racional \(\dfrac{N(x)}{D(x)}\) | Resolver \(N(x)=0\) | Descartar \(D(x)=0\) |
| Exponencial \(a^{g(x)}-c\) | Isolar: \(a^{g(x)}=c\Rightarrow g(x)=\log_a c\) | \(a>0,a\neq1\) |
| Logarítmica \(\log_a g(x)\) | \(\log_a g(x)=0 \Rightarrow g(x)=1\) | Domínio: \(g(x)>0\) |
| Módulo \(|g(x)|=c\) | Resolver \(g(x)=c\) e \(g(x)=-c\) | \(c\ge0\) |
| Produto | \(u(x)\cdot v(x)=0\Rightarrow u=0\) ou \(v=0\) | Checar domínio |
Exemplos resolvidos
1) Função afim
\(f(x)=2x-6\). Zero quando \(2x-6=0\Rightarrow x=3\).
2) Função quadrática
\(g(x)=x^2-5x+6\). \(\Delta=25-24=1\). Zeros: \(x=\dfrac{5\pm1}{2}\Rightarrow 2\) e \(3\).
3) Quadrática sem raiz real
\(h(x)=x^2+4\Rightarrow x^2=-4\) (sem solução real). Não há zero real.
4) Racional
\(p(x)=\dfrac{x-1}{x+2}\). Zeros quando o numerador zera: \(x=1\) (permitido pois \(x\neq -2\)).
5) Exponencial
\(q(x)=3^x-9=0\Rightarrow 3^x=9=3^2\Rightarrow x=2\).
6) Logarítmica
\(r(x)=\log_2(x-1)\). Zero quando \(x-1=1\Rightarrow x=2\), com domínio \(x>1\).
7) Módulo
\(s(x)=|x-4|-3=0\Rightarrow |x-4|=3\Rightarrow x-4=\pm3\Rightarrow x=1\) ou \(x=7\).
8) Produto com raiz
\(t(x)=\sqrt{x-1}\,(x-3)\). Domínio: \(x\ge1\). Zera quando \(\sqrt{x-1}=0\Rightarrow x=1\) ou \(x-3=0\Rightarrow x=3\).
➡️ Praticar zeros de funções no Banco de QuestõesExercícios (múltipla escolha) com solução
1) O zero de \(f(x)=5x-15\) é:
- \(-3\)
- \(0\)
- \(3\)
- \(15\)
Ver solução
2) Os zeros reais de \(g(x)=x^2-4x-5\) são:
- \(-1\) e \(5\)
- \(1\) e \(-5\)
- \(1\) e \(5\)
- \(-1\) e \(-5\)
Ver solução
3) Para \(p(x)=\dfrac{x+3}{x-2}\), o zero é:
- \(-3\)
- \(2\)
- \(0\)
- não existe
Ver solução
4) Resolva \(3^{x}-27=0\).
- \(x=1\)
- \(x=2\)
- \(x=3\)
- \(x=4\)
Ver solução
5) O conjunto de zeros de \(h(x)=|x+2|-4\) é:
- \(\{-6,2\}\)
- \(\{-2,4\}\)
- \(\{-6,-2\}\)
- \(\{-6,\,2\}\)
Ver solução
6) Encontre os zeros reais de \(t(x)=\ln(x-1)-\ln 2\).
- \(x=1\)
- \(x=2\)
- \(x=3\)
- \(x=0\)
Ver solução
Continue estudando
- Mapas Mentais de Matemática
- Coleção 10 eBooks de Matemática
- Banco de Questões Matemática
- Função do 2º Grau






















