Zero de uma Função Afim (Raiz)

O zero (ou raiz) de uma função afim é o valor de \(x\) que zera a função, isto é, o ponto onde o gráfico corta o eixo \(x\). Tema muito cobrado no ENEM, vestibulares e concursos.
1) Definição e fórmula
Para \( f(x)=ax+b \) com \( a\neq 0 \), o zero é obtido resolvendo \( f(x)=0 \):
- \(a\): coeficiente angular (inclinação);
- \(b\): coeficiente linear (interseção com o eixo \(y\));
- \(x_0\): abscissa do ponto onde a reta cruza o eixo \(x\).
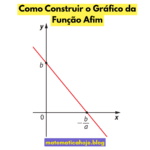
2) Interpretação gráfica
No plano cartesiano, o zero é o ponto \((x_0,0)\). Observe na imagem: a reta decrescente cruza o eixo \(x\) próxima de \(x=2\).
3) Como calcular o zero na prática
- Direto da lei da função: use \(x_0=-\dfrac{b}{a}\).
- A partir de dois pontos do gráfico: encontre \(a=\dfrac{y_2-y_1}{x_2-x_1}\), obtenha \(b\) por \(y=ax+b\) e aplique a fórmula do zero.
- Leitura no gráfico: identifique o ponto onde a reta corta o eixo \(x\).
📘 Precisa revisar fórmulas rapidamente?
Baixe o eBook Fórmulas Matemática: funções, geometria, estatística e muito mais. Perfeito para revisões de prova.
Baixar eBook de Fórmulas4) Casos especiais
- \(b=0\) ⇒ \(f(x)=ax\): zero em \(x_0=0\) (reta passa pela origem).
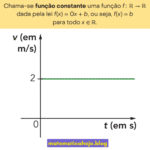
- \(a=0\) ⇒ função constante \(f(x)=b\): só tem zero se \(b=0\) (reta coincide com o eixo \(x\)).
5) Exemplo 1 — usando a fórmula \(x_0=-b/a\)
Encontre o zero de \( f(x)=-2x+4 \).
Ver solução
\(x_0=-\dfrac{b}{a}=-\dfrac{4}{-2}\)
\(x_0=2\)
Resposta: o gráfico corta o eixo \(x\) em \((2,0)\).
6) Exemplo 2 — a partir de dois pontos
A reta passa por \(A(1,2)\) e \(B(3,-2)\). Determine o zero.
Ver solução
\(a=\dfrac{-2-2}{3-1}=\dfrac{-4}{2}=-2\)
Usando \(A(1,2)\): \(2=-2\cdot 1 + b\)
\(b=4\)
\(x_0=-\dfrac{b}{a}=-\dfrac{4}{-2}=2\)
Zero: \((2,0)\).
7) Exemplo 3 — leitura no gráfico
No gráfico da imagem, a reta cruza o eixo \(x\) em \(x\approx 2\). Logo, o zero é aproximadamente \(x_0\approx 2\).
8) Exercícios (com solução no abre/fecha)
1) Calcule o zero de \(f(x)=3x-9\).
Ver solução
\(x_0=-\dfrac{-9}{3}=\dfrac{9}{3}=3\)
2) Em \(f(x)=-\dfrac{1}{2}x+5\), determine o zero.
Ver solução
\(x_0=-\dfrac{5}{-1/2}=10\)
3) A reta de \(f(x)=ax+b\) passa por \(P(0,4)\) e \(Q(2,0)\). Encontre \(a\) e o zero.
Ver solução
\(a=\dfrac{0-4}{2-0}=-2\)
De \(P\): \(4=a\cdot 0 + b \Rightarrow b=4\)
\(x_0=-\dfrac{b}{a}=-\dfrac{4}{-2}=2\)
4) Para \(f(x)=7\), o gráfico corta o eixo \(x\)?
Ver solução
Não. É função constante com \(b=7\neq 0\). Não há zero.
5) Determine o zero de \(f(x)=0,8x-1,6\).
Ver solução
Em notação decimal: \(0.8x-1.6=0\)
\(x_0=-\dfrac{-1.6}{0.8}=2\)
6) Uma tarifa custa R$ 3,00 de taxa fixa e desconto linear \(f(x)=-0,5x+3\). Para qual \(x\) o valor zera?
Ver solução
\(x_0=-\dfrac{3}{-0.5}=6\)
Com \(x=6\), \(f(x)=0\).