Está estudando conjuntos? Nesta lista completa e comentada, você encontrará 13 questões resolvidas que abordam os principais tópicos da Teoria dos Conjuntos: inclusão e não inclusão (\( \subset \), \( \not\subset \)), pertinência (\( \in \)), subconjuntos, conjuntos definidos por propriedade, conjunto vazio, relações entre conjuntos e interseções lógicas. As resoluções são explicadas passo a passo e com destaque visual, ideais para estudantes do ensino médio, ENEM e concursos públicos.
Seja para revisar, aprofundar ou aplicar o conhecimento, essa sequência de questões vai te ajudar a reforçar conceitos fundamentais e evitar os erros mais comuns que confundem até os mais experientes. Aproveite cada item, explore os detalhes das soluções e aprimore seu desempenho!
🧠 Mapas Mentais de MatemáticaQuestão 1. Escreva os conjuntos descritos em cada item:
a) O conjunto \( A \) representado pelos números naturais múltiplos de 3 menores do que 20.
b) O conjunto \( B \) representado pelos números naturais primos menores do que 27.
c) O conjunto \( C \) representado pelos números naturais menores do que 50 e múltiplos de 7.
d) \( D = \{x \mid x \text{ é satélite natural da Terra} \} \)
e) \( E = \{y \mid y \text{ é consoante da palavra “pedra”} \} \)
Ver Solução
a) Os múltiplos de 3 menores que 20 são obtidos por \(3 \times 0, 3 \times 1, 3 \times 2, \ldots\) até que o resultado seja menor que 20:
Resposta: \( A = \{0, 3, 6, 9, 12, 15, 18\} \)
b) Os números primos menores que 27 são: 2, 3, 5, 7, 11, 13, 17, 19 e 23.
Resposta: \( B = \{2, 3, 5, 7, 11, 13, 17, 19, 23\} \)
c) Os múltiplos de 7 menores que 50 são: 0, 7, 14, 21, 28, 35, 42 e 49.
Resposta: \( C = \{0, 7, 14, 21, 28, 35, 42, 49\} \)
d) O único satélite natural da Terra é a Lua.
Resposta: \( D = \{\text{Lua}\} \)
e) As letras da palavra “pedra” são: p, e, d, r, a. As consoantes são p, d e r.
Resposta: \( E = \{\text{p}, \text{d}, \text{r}\} \)
🧠 Mapas Mentais de MatemáticaQuestão 2. Dado o conjunto \( B = \{1, -1, 2, -2\} \), responda se as proposições a seguir são verdadeiras ou falsas:
a) \( 1 \in B \)
b) \( \{1\} \in B \)
c) \( 2 \in B \)
d) \( -1 \in B \)
e) \( 1 \notin B \)
f) \( 3 \in B \)
Ver Solução
a) \( 1 \in B \)? Sim, verdadeiro.
b) \( \{1\} \in B \)? Falso. O conjunto B contém o número 1, não o conjunto que tem 1 como elemento.
c) \( 2 \in B \)? Sim, verdadeiro.
d) \( -1 \in B \)? Sim, verdadeiro.
e) \( 1 \notin B \)? Falso, pois 1 está no conjunto.
f) \( 3 \in B \)? Falso, pois o número 3 não está presente.
Corrigindo as proposições falsas:
- b) \( 1 \in B \)
- e) \( 4 \notin B \)
- f) \( 3 \notin B \)
Questão 3. Considere o conjunto \( A = \{3, 4, 5, 6, 7, 8, 9, 10, 11\} \).
Represente os subconjuntos de \( A \) formados:
a) Pelos números maiores do que 5 e menores do que 10.
b) Pelos números pares.
c) Pelos números ímpares maiores do que ou iguais a 7.
Ver Solução
a) Procuramos os elementos de \( A \) que estão no intervalo \( (5, 10) \):
Elementos: 6, 7, 8, 9
Subconjunto: \( \{6, 7, 8, 9\} \)
b) Os números pares no conjunto \( A \) são aqueles divisíveis por 2:
Elementos: 4, 6, 8, 10
Subconjunto: \( \{4, 6, 8, 10\} \)
c) Agora buscamos os números ímpares maiores ou iguais a 7:
Elementos: 7, 9, 11
Subconjunto: \( \{7, 9, 11\} \)
🧠 Mapas Mentais de MatemáticaQuestão 4. Dado o conjunto \( E = \{2, 4, 6, 8\} \), liste todos os subconjuntos de \( E \) formados por:
a) 3 elementos
b) 4 elementos
Ver Solução
a) Para formar subconjuntos de 3 elementos, fazemos combinações de 4 elementos tomados 3 a 3.
As possíveis combinações são:
- {2, 4, 6}
- {2, 4, 8}
- {2, 6, 8}
- {4, 6, 8}
b) O único subconjunto com 4 elementos é o próprio conjunto:
{2, 4, 6, 8}
🧠 Mapas Mentais de MatemáticaQuestão 5. Sejam \( a \) e \( b \) números naturais. Determine o valor de \( a + b \), tal que:
\( \{0, 1, 2\} = \{2, a, b\} \)
Ver Solução
A igualdade entre conjuntos implica que ambos devem conter exatamente os mesmos elementos, embora em ordens diferentes.
O conjunto à esquerda é \( \{0, 1, 2\} \).
O conjunto à direita é \( \{2, a, b\} \), ou seja, contém o número 2 e mais dois números \( a \) e \( b \).
Sabemos que o número 2 já está presente nos dois conjuntos, então os elementos que faltam em \( \{a, b\} \) para formar o conjunto \( \{0, 1, 2\} \) são:
0 e 1
Logo, \( a = 0 \) e \( b = 1 \) (ou vice-versa).
Portanto,
\( a + b = 0 + 1 = \)1
🧠 Mapas Mentais de MatemáticaQuestão 6. Uma pessoa tem quatro opções de música para escutar: a, b, c e d. Considerando o conjunto \( \{a, b, c, d\} \) formado por essas músicas, resolva os itens:
a) Indique todos os subconjuntos possíveis com apenas duas músicas.
b) Se uma pessoa quiser ouvir apenas duas músicas por dia, quantas possibilidades de pares ela tem para escolher?
Ver Solução
a) Para listar todos os subconjuntos com duas músicas, usamos a ideia de combinações de 4 elementos tomados 2 a 2, sem repetição e sem ordem:
- {a, b}
- {a, c}
- {a, d}
- {b, c}
- {b, d}
- {c, d}
b) A quantidade de pares possíveis é dada por:
\( C(4,2) = \dfrac{4!}{2!(4-2)!} = \dfrac{4 \cdot 3}{2 \cdot 1} = \)6
Resposta: 6 pares
🧠 Mapas Mentais de MatemáticaQuestão 7. No diagrama a seguir, \( A \), \( B \) e \( C \) são três conjuntos não vazios.
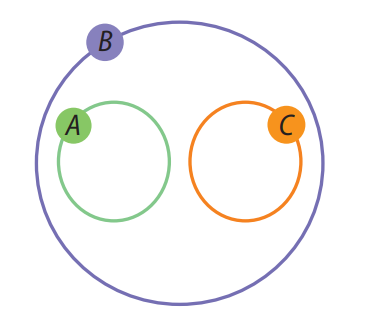
Associe V ou F a cada uma das seguintes sentenças, conforme ela seja verdadeira ou falsa:
- a) \( A \subset B \)
- b) \( C \subset B \)
- c) \( B \subset A \)
- d) \( A \subset C \)
- e) \( B \not\subset A \)
- f) \( A \subset C \)
- g) \( B \supset A \)
- h) \( A \not\supset B \)
Ver Solução
a) \( A \subset B \): V – A está totalmente dentro de B.
b) \( C \subset B \): V – C também está contido em B.
c) \( B \subset A \): F – B contém A, não o contrário.
d) \( A \subset C \): F – A e C não têm interseção visível, logo A não está dentro de C.
e) \( B \not\subset A \): V – B não está contido em A.
f) \( A \subset C \): F – Repetida da d), ainda falsa.
g) \( B \supset A \): V – Sim, B contém A.
h) \( A \not\supset B \): V – A não contém B, é o contrário.
🧠 Mapas Mentais de MatemáticaQuestão 8. Dados os conjuntos:
- \( A = \{1\} \)
- \( B = \{0, 1\} \)
- \( C = \{1, 2, 3\} \)
- \( D = \{0, 1, 2, 4\} \)
Relacione cada par de conjuntos a seguir usando o símbolo \( \subset \) (subconjunto) ou \( \not\subset \) (não subconjunto):
- a) \( A \) e \( B \)
- b) \( A \) e \( C \)
- c) \( A \) e \( D \)
- d) \( B \) e \( C \)
- e) \( B \) e \( D \)
- f) \( C \) e \( D \)
Ver Solução
a) \( A \subset B \): V – 1 está em B.
b) \( A \subset C \): V – 1 também está em C.
c) \( A \subset D \): V – 1 também está em D.
d) \( B \subset C \): F – B tem o 0, que não pertence a C.
e) \( B \subset D \): V – 0 e 1 estão em D.
f) \( C \subset D \): F – 3 pertence a C, mas não está em D.
🧠 Mapas Mentais de MatemáticaQuestão 9. Sejam \( A \), \( B \) e \( C \) os conjuntos a seguir:
\( A = \{x \mid x \text{ é número natural par compreendido entre 3 e 15}\}; \)
\( B = \{x \mid x \text{ é número natural par menor do que 15}\}; \)
\( C = \{x \mid x \text{ é número natural par diferente de 2}\}. \)
Relacione cada par a seguir usando o símbolo \( \subset \) ou \( \not\subset \).
- a) A e B
- b) A e C
- c) B e C
Ver Solução
a) Vamos descrever os elementos de A e B:
\( A = \{4, 6, 8, 10, 12, 14\} \)
\( B = \{0, 2, 4, 6, 8, 10, 12, 14\} \)
Todos os elementos de A estão em B → \( A \subset B \)
b) Agora vejamos A e C:
\( C = \{x \in \mathbb{N} \mid x \text{ par e } x \ne 2\} = \{0, 4, 6, 8, 10, 12, 14, 16, \ldots\} \)
Como todos os elementos de A também estão em C → \( A \subset C \)
c) Analisando B e C:
\( B \) contém o número 2, mas \( C \) exclui esse número.
Logo, 2 está em B, mas não está em C → \( B \not\subset C \)
🧠 Mapas Mentais de MatemáticaQuestão 10. Dado o conjunto \( A = \{0, 2, 3\} \), diga se as proposições são verdadeiras ou falsas.
- \( 0 \in A \)
- \( 1 \subset A \)
- \( 3 \in A \)
- \( \{3\} \subset A \)
- \( \{1, 2\} \subset A \)
- \( \emptyset \subset A \)
- \( \emptyset \in A \)
- \( \{3\} \in A \)
Ver Solução
a) \( 0 \in A \): V – O número 0 está no conjunto A.
b) \( 1 \subset A \): F – 1 não é um conjunto, é um número. A notação está incorreta.
c) \( 3 \in A \): V – 3 está no conjunto A.
d) \( \{3\} \subset A \): V – O conjunto unitário \{3\} está contido em A.
e) \( \{1, 2\} \subset A \): F – 1 não pertence a A, logo \{1, 2\} não está contido em A.
f) \( \emptyset \subset A \): V – O conjunto vazio é subconjunto de qualquer conjunto.
g) \( \emptyset \in A \): F – O conjunto vazio não está como elemento de A.
h) \( \{3\} \in A \): F – A contém o número 3, não o conjunto \{3\}.
🧠 Mapas Mentais de MatemáticaQuestão 11. Indique apenas as afirmações verdadeiras.
- \( \{5\} \subset \{0, 5, 10, 15\} \)
- \( \{a, b, c\} \supset \{b, a, c\} \)
- \( 2 \subset \{0, 2, 4\} \)
- \( 8 \in \{2, 4, 6, 8, 10\} \)
- \( \{1, 2, 3\} \supset \{1, 2\} \)
- \( \{-1, 6\} \not\subset \{n \mid n \text{ é um número natural} \} \)
- \( 3 \in \{0, 3, 6, 9\} \)
- \( \frac{1}{2} \notin \{n \mid n \text{ é um número natural} \} \)
Ver Solução
a) \( \{5\} \subset \{0, 5, 10, 15\} \): V – O elemento 5 está presente no segundo conjunto.
b) \( \{a, b, c\} \supset \{b, a, c\} \): V – Os conjuntos são iguais, logo cada um é subconjunto e também superconjunto do outro.
c) \( 2 \subset \{0, 2, 4\} \): F – 2 é um número, não um conjunto. O correto seria \( 2 \in \).
d) \( 8 \in \{2, 4, 6, 8, 10\} \): V – 8 pertence ao conjunto dado.
e) \( \{1, 2, 3\} \supset \{1, 2\} \): V – Os elementos de \{1, 2\} estão contidos no outro conjunto.
f) \( \{-1, 6\} \not\subset \{n \in \mathbb{N} \} \): V – -1 não é número natural.
g) \( 3 \in \{0, 3, 6, 9\} \): V – Está presente no conjunto.
h) \( \frac{1}{2} \notin \{n \mid n \text{ é número natural} \} \): V – Meio não é número natural.
Alternativas verdadeiras: a, b, d, e, f, g, h
🧠 Mapas Mentais de MatemáticaQuestão 12. Sendo \( P \) e \( Q \) dois conjuntos não vazios, de modo que \( P \subset Q \), indique apenas as afirmações verdadeiras.
- Existe \( x \in P \), tal que \( x \notin Q \)
- Existe \( x \in Q \), tal que \( x \notin P \)
- Se \( x \in Q \), então \( x \in P \)
- Se \( x \notin Q \), então \( x \notin P \)
- \( P \) e \( Q \) não têm elementos em comum.
Ver Solução
a) F – Se \( P \subset Q \), então todo elemento de P também está em Q. Logo, não existe elemento de P fora de Q. F
b) V – Como \( P \subset Q \), Q tem mais elementos que P. Portanto, pode haver \( x \in Q \) que não está em P. V
c) F – Nem todo elemento de Q está em P, pois \( P \subset Q \). A inclusão é unilateral. F
d) V – Se \( x \notin Q \), então ele não pode estar em P, pois todos os elementos de P estão dentro de Q. V
e) F – Pelo contrário, \( P \subset Q \) significa que todos os elementos de P estão em Q. Eles têm elementos em comum. F
Alternativa correta: d
🧠 Mapas Mentais de MatemáticaQuestão 13. Quantos conjuntos \( M \) satisfazem à sentença:
\( \{1, 2\} \subset M \subset \{1, 2, 3, 4\} \)
Ver Solução
Queremos contar quantos conjuntos \( M \) existem tal que:
- Contenham obrigatoriamente os elementos 1 e 2.
- Sejam subconjuntos de \( \{1, 2, 3, 4\} \), mas diferentes dele.
Isso significa que \( M \) pode conter 1 e 2 e mais alguns elementos de \{3, 4\}, mas não pode conter todos, senão seria igual ao conjunto total.
Os elementos “livres” para adicionar ou não são: 3 e 4 (dois elementos).
Total de subconjuntos possíveis com esses dois elementos é \( 2^2 = 4 \), mas devemos excluir o caso em que nenhum é adicionado (pois \( M \) seria igual a \( \{1, 2\} \), e não estritamente maior), e também excluir o caso com os dois juntos (pois \( M = \{1, 2, 3, 4\} \), e não estritamente menor).
Conjuntos válidos:
- \( \{1, 2, 3\} \)
- \( \{1, 2, 4\} \)
- \( \{1, 2, 3, 4\} \) → não serve
- \( \{1, 2\} \) → não serve
Resposta final: 4 conjuntos
🧠 Mapas Mentais de MatemáticaQuestão 14. Qual deve ser a relação entre os conjuntos \( A \), \( B \) e \( C \) para que:
\( A \subset B \), \( B \subset C \) e \( C \subset A \)?
Ver Solução
Temos uma cadeia de inclusões:
- \( A \subset B \)
- \( B \subset C \)
- \( C \subset A \)
Juntando todas as relações, temos:
\( A \subset B \subset C \subset A \)
Ou seja, cada conjunto está contido no próximo, até fechar em \( A \).
Isso só é possível se todos forem iguais. Afinal, um conjunto só pode estar contido no outro e ainda conter o outro se eles forem exatamente iguais.
Resposta final: \( A = B = C \)
🧠 Mapas Mentais de Matemática