O cone é uma figura geométrica tridimensional caracterizada por uma base circular e uma superfície lateral que converge em um ponto chamado vértice. Sua estrutura é frequentemente comparada a objetos do cotidiano, como um chapéu de festa ou um sorvete de casquinha. Neste artigo, vamos explorar em detalhes as propriedades do cone, abordando área da base, área lateral, área total, volume, relação métrica, planificação e o cone equilátero.
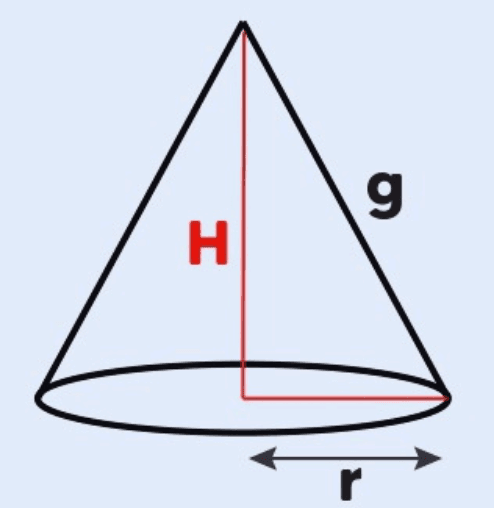
Área da Base
A base de um cone é um círculo, e a área da base Ab pode ser calculada pela fórmula da área do círculo:
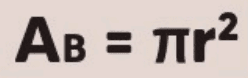
onde:
- r é o raio da circunferência da base.
Questão: Um cone possui uma base com raio de 5 cm. Qual é a área da base desse cone?
Solução: Para calcular a área da base, utilizamos a fórmula da área do círculo:
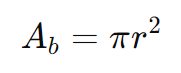
Substituindo o valor do raio r=5 cm:
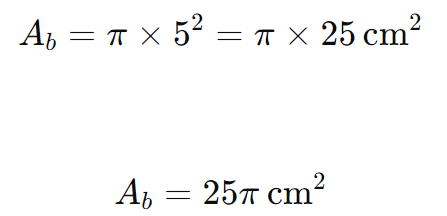
Portanto, a área da base é 25π cm2.
Área Lateral
A área lateral Al do cone é a área da superfície curva que vai da borda da base até o vértice. Essa área pode ser calculada usando a fórmula:
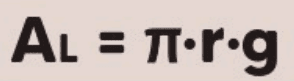
onde:
- g é a geratriz, que representa a distância do vértice à borda da base do cone.
A geratriz pode ser encontrada utilizando o Teorema de Pitágoras na relação métrica que será abordada a seguir.
Questão: Um cone possui um raio de base de 3 cm e uma geratriz de 5 cm. Qual é a área lateral desse cone?
Solução: A área lateral do cone é dada por:
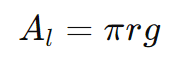
Substituindo os valores de r=3 cm e g=5 cm:
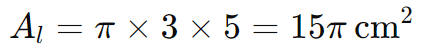
Portanto, a área lateral do cone é 15π cm2.
Área Total
A área total At do cone é a soma da área da base e da área lateral:
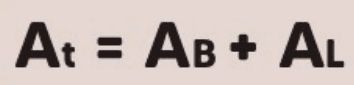
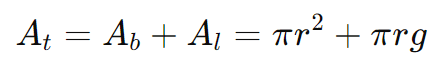
Essa fórmula considera tanto a superfície plana da base quanto a superfície curva lateral do cone.
Questão: Um cone tem raio da base de 4 cm e geratriz de 6 cm. Qual é a área total desse cone?
Solução: A área total do cone é a soma da área da base e da área lateral:
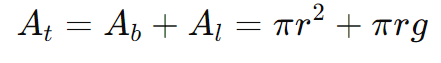
Substituindo os valores r=4 cm e g=6 cm:
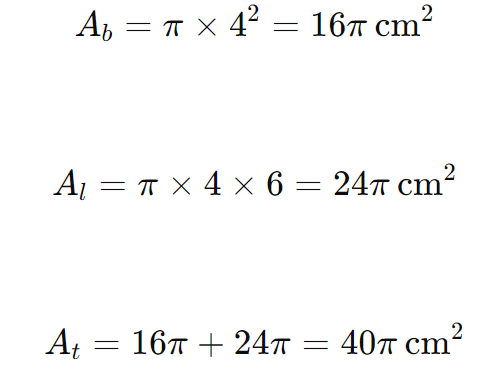
Portanto, a área total do cone é 40π cm2.
Volume
O volume V de um cone pode ser calculado pela fórmula:
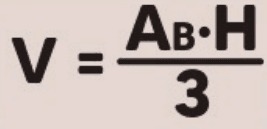
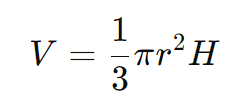
onde:
- H é a altura do cone, que corresponde à distância do vértice até o centro da base.
Essa fórmula reflete que o volume de um cone é um terço do volume de um cilindro com a mesma base e altura.
Questão: Um cone tem uma altura de 12 cm e um raio da base de 7 cm. Qual é o volume desse cone?
Solução: O volume do cone é calculado pela fórmula:
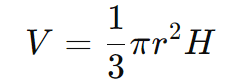
Substituindo os valores r=7 cm e H=12 cm:
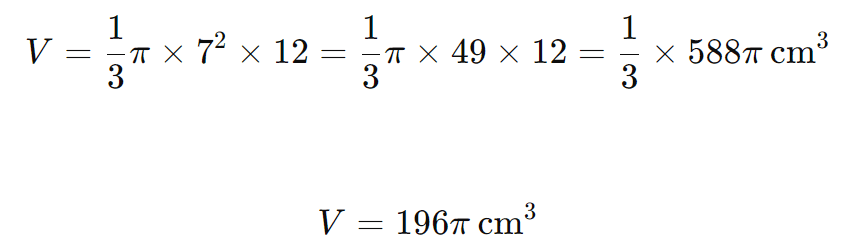
Portanto, o volume do cone é 196π cm3.
Relação Métrica
No cone, a geratriz g, a altura H e o raio da base r estão relacionados pelo Teorema de Pitágoras, formando um triângulo retângulo:

Essa relação é fundamental para encontrar a geratriz quando se conhece a altura e o raio, ou vice-versa.
Questão: Em um cone, o raio da base mede 8 cm e a altura é de 15 cm. Qual é o comprimento da geratriz desse cone?
Solução: A relação métrica entre o raio, a altura e a geratriz é dada por:
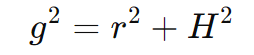
Substituindo os valores r=8 cm e H=15 cm:
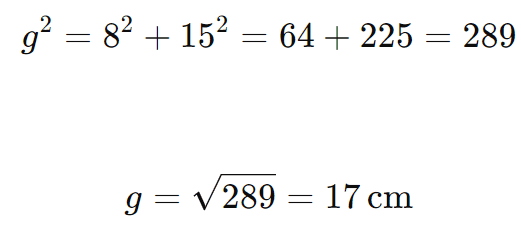
Portanto, a geratriz do cone é 17 cm.
Planificação
A planificação de um cone envolve “abrir” sua superfície lateral em um setor circular e manter a base como um círculo. Ao desenrolar a lateral do cone, o setor circular resultante tem raio igual à geratriz g do cone e arco igual ao comprimento da circunferência da base, que é 2πr.
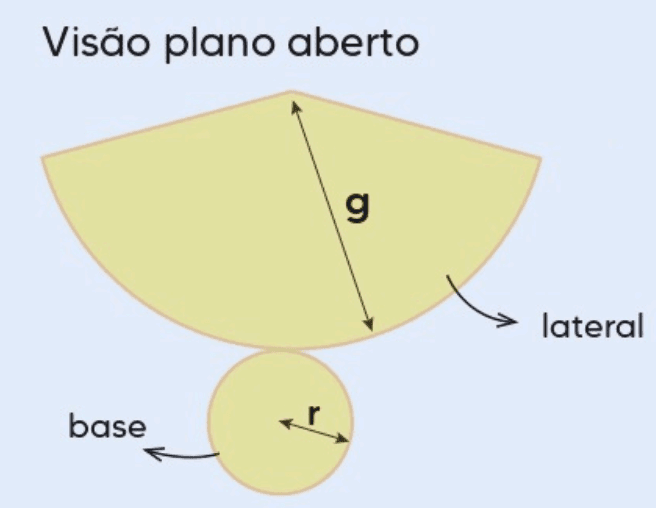
Questão: Um cone possui raio da base de 6 cm e geratriz de 10 cm. Qual será o raio e o ângulo do setor circular formado pela planificação da superfície lateral?
Solução: O raio do setor circular formado pela planificação da superfície lateral do cone é igual à geratriz g=10 cm.
Para encontrar o ângulo do setor, utilizamos a relação:
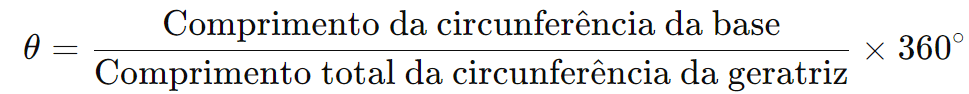
O comprimento da circunferência da base é:
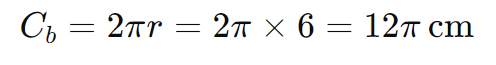
O comprimento total da circunferência da geratriz (se fosse completa) seria:
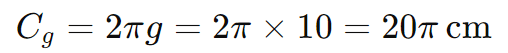
Então, o ângulo θ é:
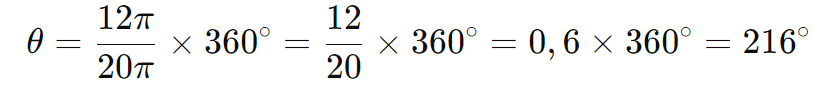
Portanto, o raio do setor circular é 10 cm e o ângulo do setor é 216°
.
Cone Equilátero
Um cone equilátero é aquele em que a geratriz g é igual ao diâmetro da base, ou seja, g=2rg = 2rg=2r. Nesse caso, a altura H e o raio r estão relacionados por: H=r√3

Isso significa que a altura de um cone equilátero é √3 vezes o raio da base. O cone equilátero tem propriedades específicas que o tornam interessante em estudos de geometria, especialmente na relação entre suas dimensões e na planificação.
Questão: Um cone equilátero possui uma geratriz de 10 cm. Qual é a altura desse cone?
Solução: Para um cone equilátero, a geratriz é igual ao diâmetro da base:
g=2r
Sendo assim, o raio r é:
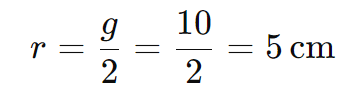
A altura H de um cone equilátero é dada por:
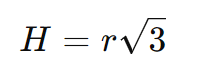
Substituindo o valor de r=5 cm:
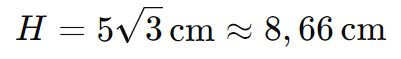
Portanto, a altura do cone equilátero é aproximadamente 8,66 cm.
Conclusão
O cone é uma figura geométrica rica em propriedades e aplicações. Compreender suas fórmulas de área, volume e as relações métricas é fundamental para resolver problemas práticos e teóricos envolvendo essa forma. Seja em matemática ou em disciplinas que utilizam geometria espacial, como física e engenharia, o cone desempenha um papel essencial.
Leia também
O Cubo: Propriedades e Fórmulas Essenciais
O Paralelepípedo: Propriedades e Fórmulas Essenciais
Pirâmides: Propriedades, Fórmulas e Aplicações
Tetraedro Regular: Propriedades, Fórmulas e Aplicações
Tronco de Pirâmide: Propriedades, Fórmulas e Proporções
Cilindro: Conceitos e Cálculos
Cone: Tudo o Que Você Precisa Saber
Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão













