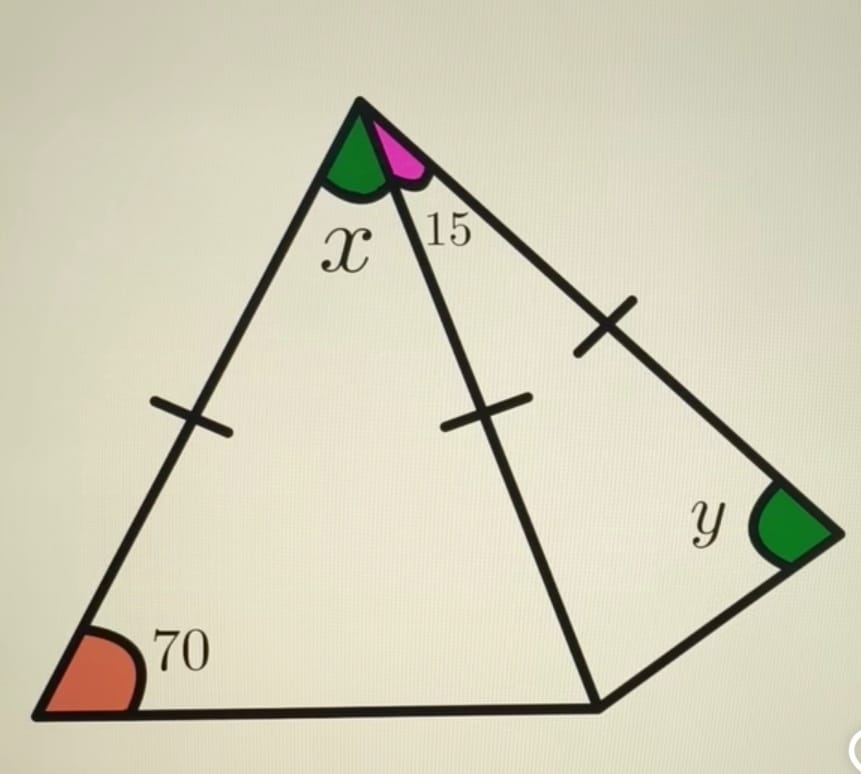
Em um triângulo isósceles, o ângulo da base mede 70°. Dentro deste triângulo, forma-se um segundo triângulo menor isósceles, onde um dos ângulos internos mede 15°, conforme mostrado na figura. Determine os valores dos ângulos x (no vértice do triângulo menor) e y (um dos ângulos da base do triângulo menor).
Alternativas:
a) x = 50° e y = 80°
b) x = 40° e y = 82,5°
c) x = 45° e y = 85,2°
d) x = 35° e y = 75,5°
Ver Solução
Vamos determinar os valores de x e y com base no problema apresentado.
Passo 1: Analisar o triângulo maior
O triângulo maior é isósceles, com o ângulo da base 70°. Sabemos que a soma dos ângulos internos de um triângulo é 180°. Assim, os dois ângulos da base são iguais.
Ângulo do vértice = 180° – 70° – 70° = 40°
Portanto, o ângulo xx, que corresponde ao ângulo do vértice do triângulo menor, é:
x = 40°
Passo 2: Determinar o valor de y
O ângulo y está no triângulo menor, e sabemos que a soma dos ângulos internos do triângulo também é 180°. A equação para y fica:
y + y + 15° = 180°
Simplificando:
2y + 15° = 180°
2y = 165°
y = 82,5°
Resumo Final:
- x=40°
- y=82,5°
Alternativa B
Gostou dessa questão? Que tal desafiar ainda mais seus conhecimentos? Clique aqui e resolva outra questão matemática preparada especialmente para você! 📚✨
👉Entre no nosso canal do WhatsApp
🟢Mapas Mentais de Matemática para Concurso
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Pronto para mergulhar em mais desafios matemáticos? 🚀 Explore nossa categoria completa com diversas questões matemática para testar e aprimorar seus conhecimentos! Clique aqui e comece agora! 📘✔️”
