A Análise Combinatória é o ramo da Matemática responsável por estudar métodos para contar elementos de forma inteligente, sem precisar listar todas as possibilidades. Isso se torna essencial em provas, concursos e aplicações práticas da vida real.
Neste artigo, você encontrará a teoria bem explicada, fórmulas destacadas, exemplos contextualizados, exercícios resolvidos passo a passo e questões extras para treinar.
✅ Princípio da Multiplicação
O que é?
Quando uma tarefa é dividida em etapas independentes, devemos multiplicar o número de possibilidades de cada etapa.
Fórmula:
Total = opções₁ × opções₂ × … × opçõesₙ
Exemplos:
Exemplo 1:
Quantas senhas podem ser formadas com 2 letras (A-Z) seguidas de 2 números (0-9)?
Solução:
Letras: 26 opções para cada → 26 × 26
Números: 10 opções para cada → 10 × 10
Total: 26 × 26 × 10 × 10 = 67.600
Exemplo 2:
Um combo é formado por 4 tipos de hambúrguer, 3 tipos de batata e 5 refrigerantes. Quantos combos diferentes posso montar?
Solução: 4 × 3 × 5 = 60
➕ Princípio da Adição
O que é?
Usado quando se pode realizar uma coisa ou outra, mas não ambas ao mesmo tempo. Somamos as opções.
Fórmula:
Total = opções₁ + opções₂ + … + opçõesₙ
Exemplos:
Exemplo 1:
Uma pessoa pode escolher entre 3 peças de teatro ou 4 filmes.
Total = 3 + 4 = 7 possibilidades
Exemplo 2:
Uma lanchonete oferece 6 tipos de suco ou 5 tipos de chá.
Total = 6 + 5 = 11 opções
🔁 Permutação Simples
O que é?
Número de formas de organizar todos os elementos de um conjunto, sem repetição.
Fórmula:
Pₙ = n!
(n fatorial é o produto de todos os inteiros de 1 até n)
Exemplos:
Exemplo 1:
Quantas formas diferentes posso organizar 5 livros na estante?
P₅ = 5! = 5×4×3×2×1 = 120
Exemplo 2:
Quantos anagramas diferentes da palavra “FIM”?
P₃ = 3! = 6
🔁 Permutação com Repetição
O que é?
Quando há elementos repetidos, precisamos dividir o fatorial total pelas repetições.
Fórmula:
P = n! / (a! × b! × …)
Onde a, b… são as quantidades de elementos repetidos.
Exemplos:
Exemplo 1:
Quantos anagramas da palavra “COCO”?
Temos 4 letras, com 2 C e 2 O → 4! / (2! × 2!) = 24 / 4 = 6
Exemplo 2:
Quantas formas distintas com “SALAS”?
Temos: S (2x), A (2x), L (1x) → 5! / (2! × 2!) = 120 / 4 = 30
🧮 Arranjo Simples
O que é?
Quando escolhemos parte dos elementos, com ordem e sem repetição.
Fórmula:
Aₙ,ₚ = n! / (n – p)!
Exemplos:
Exemplo 1:
De 8 candidatos, de quantas formas diferentes posso escolher um presidente, vice e secretário?
A₈,₃ = 8! / (8 – 3)! = 8 × 7 × 6 = 336
Exemplo 2:
Quantas senhas diferentes posso formar com 4 dígitos distintos de 0 a 9?
A₁₀,₄ = 10 × 9 × 8 × 7 = 5.040
🔢 Combinação Simples
O que é?
Escolha de parte dos elementos, sem ordem e sem repetição.
Fórmula:
Cₙ,ₚ = n! / [p!(n – p)!]
Exemplos:
Exemplo 1:
Quantas duplas diferentes posso formar entre 6 pessoas?
C₆,₂ = 6! / (2! × 4!) = 720 / 48 = 15
Exemplo 2:
De 10 questões, escolher 4 para responder:
C₁₀,₄ = 210
🧠 Quadro Comparativo
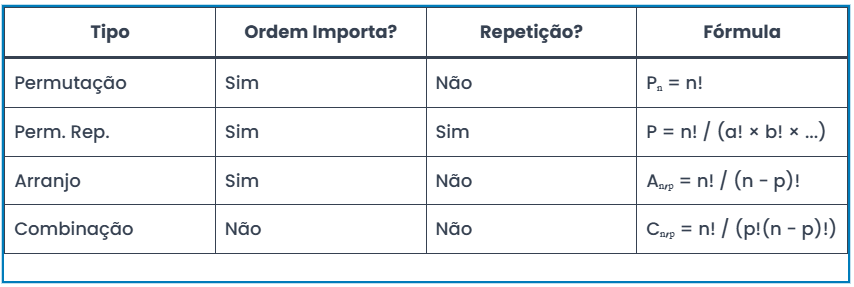
🧪 Exercícios Resolvidos
1. Quantas senhas com 3 letras (sem repetir) posso formar com as letras A, B, C, D, E?
Solução: Arranjo de 3 entre 5 →
A₅,₃ = 5 × 4 × 3 = 60
2. Quantas comissões de 4 pessoas posso montar com 10 candidatos?
Solução: Combinação →
C₁₀,₄ = 210
3. Quantos anagramas a palavra TATA possui?
T: 2 letras | A: 2 letras →
P = 4! / (2!2!) = 24 / 4 = 6 anagramas
4. Um combo inclui: 3 tipos de lanche, 2 tipos de suco e 4 tipos de sobremesa. Quantos combos posso formar?
Princípio multiplicativo: 3 × 2 × 4 = 24 combos
📝 Desafio para você
- Quantos anagramas tem a palavra “ARARA”?
- Quantas comissões de 3 pessoas podem ser formadas entre 7 pessoas?
- De quantas formas diferentes posso distribuir 3 prêmios entre 10 pessoas?
Quer as soluções comentadas? Comente abaixo ou baixe nosso eBook gratuito com 50 exercícios resolvidos de Análise Combinatória!
📥 Baixe também:
📚 Ebook Gratuito: “Power Point de Análise Combinatória”
👉 Clique aqui para baixar agora
