Questão 10
A prefeitura de uma cidade planeja construir três postos de saúde. Esses postos devem ser construídos em locais equidistantes entre si e de forma que as distâncias desses três postos ao hospital da cidade sejam iguais.
Foram conseguidos três locais para a construção dos postos que apresentam as características desejadas, e que distam 10 km entre si, conforme o esquema abaixo:
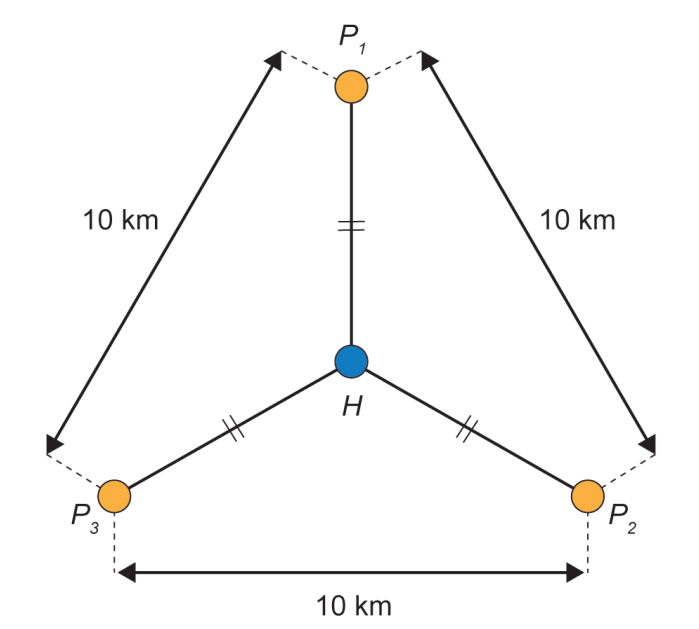
O ponto \( H \) representa o hospital e os pontos \( P_1, P_2, P_3 \) são os postos de saúde. Esses quatro pontos estão em um mesmo plano.
A distância, em quilômetro, entre o hospital e cada um dos postos de saúde, é um valor entre:
- A) 2 e 3
- B) 4 e 5
- C) 5 e 6
- D) 7 e 8
- E) 8 e 9
1. Interpretação:
Os postos formam um triângulo equilátero de lado 10 km, e o hospital está no ponto que tem a mesma distância para os três vértices, ou seja, o centro do triângulo equilátero.
—2. Fórmula da altura de um triângulo equilátero:
\[ h = \frac{l \cdot \sqrt{3}}{2} \quad \text{com } l = 10 \Rightarrow h = \frac{10 \cdot \sqrt{3}}{2} = 5\sqrt{3} \]
3. Distância do centro ao vértice (circuncentro):
\[ \text{Distância} = \frac{2}{3} \cdot h = \frac{2}{3} \cdot 5\sqrt{3} = \frac{10\sqrt{3}}{3} \]
4. Aproximação com \( \sqrt{3} \approx 1{,}73 \):
\[ \frac{10 \cdot 1{,}73}{3} \approx \frac{17{,}3}{3} \approx 5{,}77 \]
—5. Verificação da alternativa:
Como \( 5{,}77 \) está entre 5 e 6, a resposta correta é:
Resposta correta: Letra C
[/toggle]












