Distância entre Dois Pontos

Distância entre Dois Pontos – Fórmula, Exemplos e Exercícios

A distância entre dois pontos é um dos conceitos fundamentais da geometria analítica. Com ela, podemos determinar o comprimento do segmento de reta que liga dois pontos no plano cartesiano. Esse cálculo é muito utilizado em física, engenharia, design gráfico e também em provas de matemática de concursos e vestibulares.

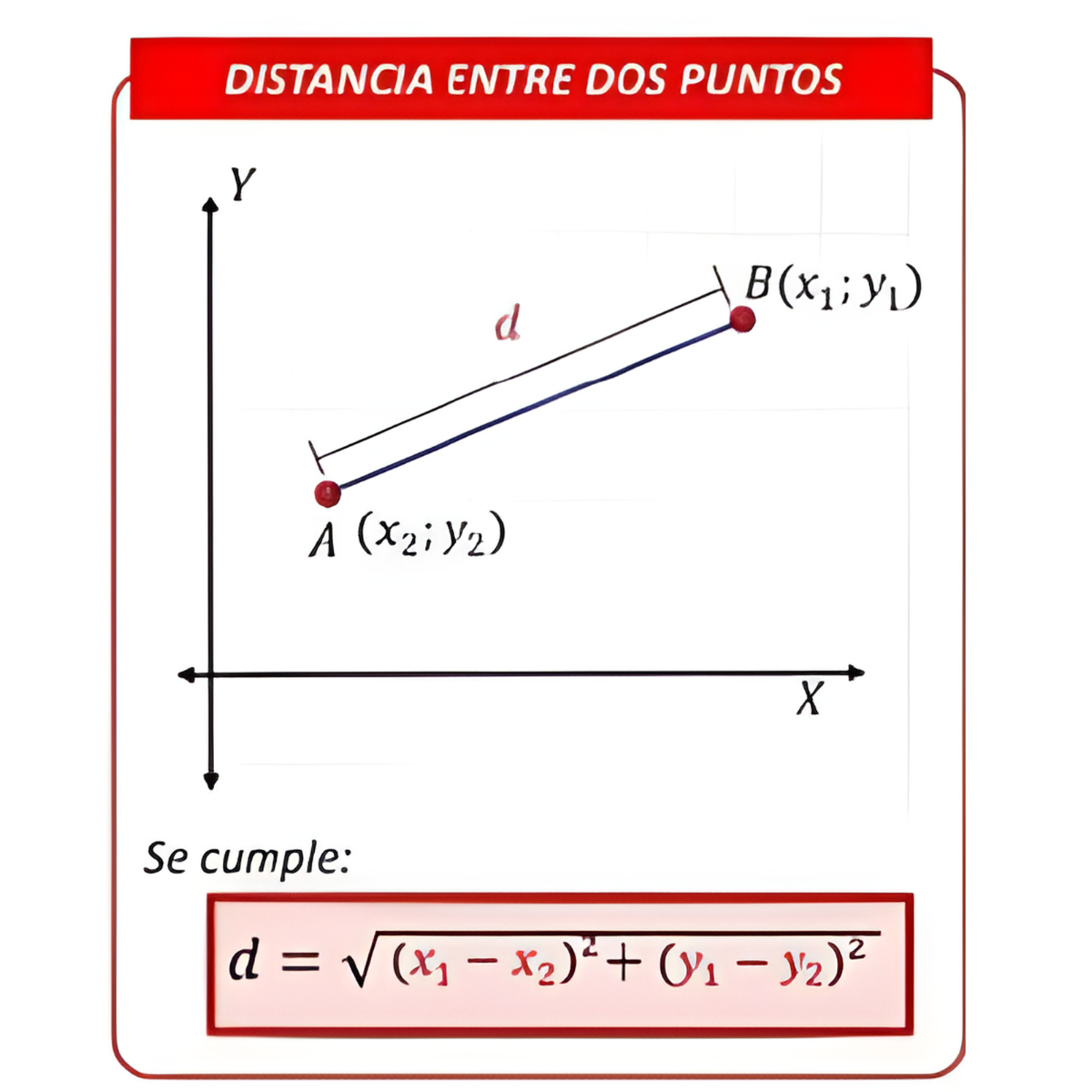
Fórmula da distância entre dois pontos no plano cartesiano

📘 O que é a Distância entre Dois Pontos

Dados dois pontos A e B em um plano cartesiano, com coordenadas:

\( A(x_1, y_1) \) e \( B(x_2, y_2) \),

a distância entre esses pontos representa o comprimento do segmento de reta que os conecta.

📏 Fórmula da Distância entre Dois Pontos

\( d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} \)

Essa expressão deriva do teorema de Pitágoras, aplicando-o ao triângulo retângulo formado pela diferença entre as coordenadas dos dois pontos.

🧩 Exemplo Resolvido

Exemplo: Calcule a distância entre os pontos \( A(2, 3) \) e \( B(8, 6) \).

Solução:

Substituindo os valores na fórmula:

\( d = \sqrt{(8 – 2)^2 + (6 – 3)^2} \)
\( d = \sqrt{6^2 + 3^2} \)
\( d = \sqrt{36 + 9} \)
\( d = \sqrt{45} \)
\( d = 3\sqrt{5} \)

Resposta: A distância entre A e B é \( 3\sqrt{5} \) unidades.

📘 Quer todas as fórmulas de Matemática em um só lugar?
👉 Baixe gratuitamente o eBook Fórmulas Matemática

🧮 Lista de Exercícios

1. Calcule a distância entre os pontos \( A(0, 0) \) e \( B(3, 4) \).

\( d = \sqrt{(3 – 0)^2 + (4 – 0)^2} = \sqrt{9 + 16} = 5 \)

2. Determine a distância entre \( A(-2, 5) \) e \( B(4, -3) \).

\( d = \sqrt{(4 – (-2))^2 + (-3 – 5)^2} = \sqrt{6^2 + (-8)^2} = \sqrt{36 + 64} = 10 \)

3. Encontre a distância entre \( A(7, -2) \) e \( B(1, 4) \).

\( d = \sqrt{(1 – 7)^2 + (4 – (-2))^2} = \sqrt{(-6)^2 + 6^2} = \sqrt{72} = 6\sqrt{2} \)

4 (Múltipla Escolha). A distância entre os pontos \( A(2, -1) \) e \( B(6, 2) \) é:

A) 4
B) 5
C) \( \sqrt{10} \)
D) \( \sqrt{25} \)

\( d = \sqrt{(6 – 2)^2 + (2 – (-1))^2} = \sqrt{4^2 + 3^2} = \sqrt{25} = 5 \) ✅ Alternativa correta: B)

5 (Desafio ENEM). Um drone parte do ponto \( A(3, 2) \) e vai até o ponto \( B(9, 8) \). Qual é a distância percorrida?

\( d = \sqrt{(9 – 3)^2 + (8 – 2)^2} = \sqrt{36 + 36} = \sqrt{72} = 6\sqrt{2} \)

📚 Continue Estudando

Relacionadas

Equação Geral da Reta

Inclinação da Reta (Coeficiente Angular)

Coordenadas do Baricentro

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.