Desigualdade Triangular — condição para formar triângulo
Para três segmentos \(a\), \(b\) e \(c\) formarem um triângulo, cada lado deve ser menor que a soma dos outros dois e maior que o valor absoluto de sua diferença.
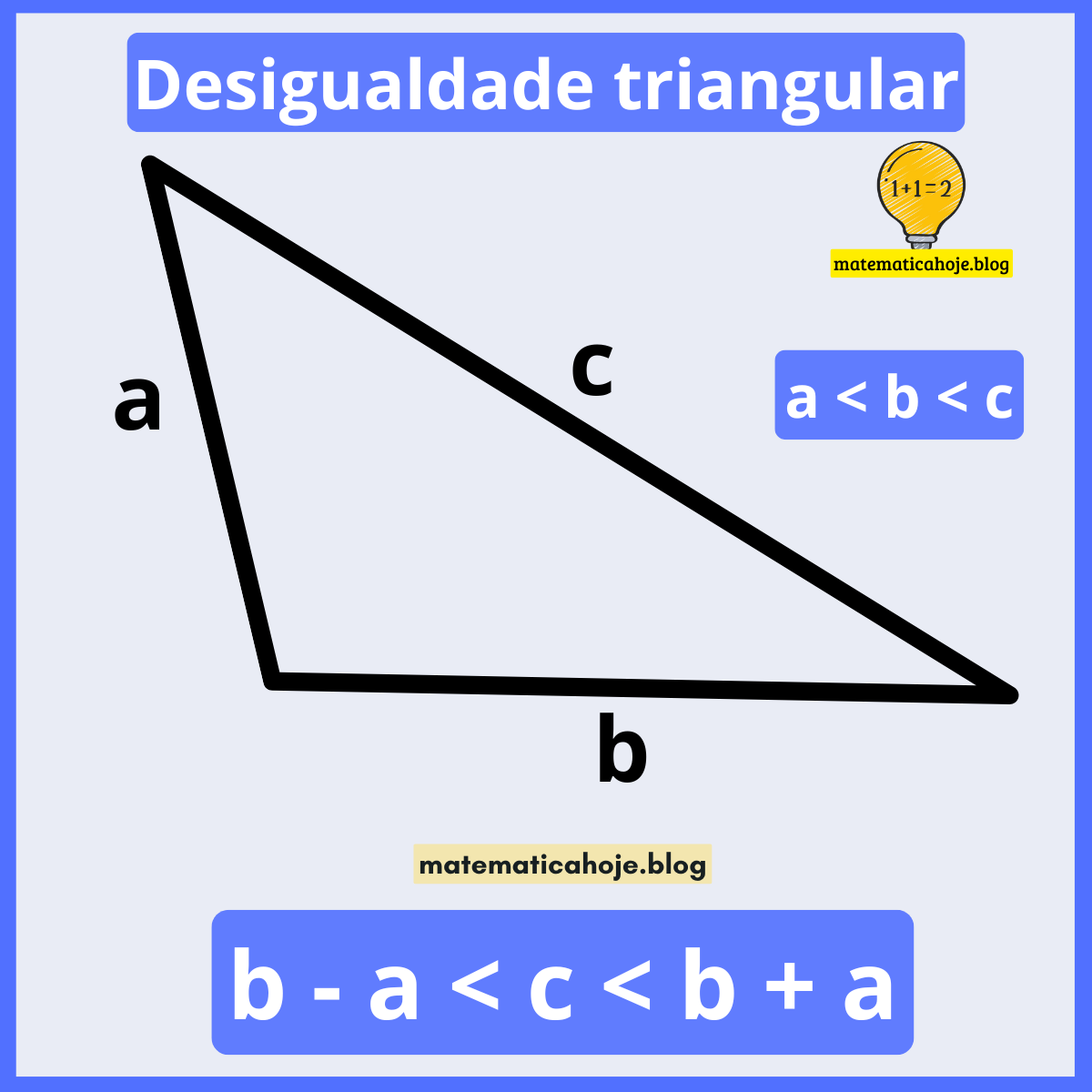
Especificamente para o lado \(c\): \( |b-a| < c < a+b \). A propriedade vale de modo cíclico para \(a\) e \(b\).
Essas ideias se conectam aos ângulos do triângulo: confira a Soma dos Ângulos Internos, a Soma dos Ângulos Externos e o Teorema do Ângulo Externo.
Intuição geométrica
Se um lado fosse maior ou igual à soma dos outros dois, os segmentos “esticariam” sem se encontrar, não fechando o triângulo. Se um lado fosse menor ou igual à diferença dos outros, um deles “encobriria” o outro, também impedindo o fechamento.
Mapas Mentais de Matemática — Destaque
Revisão visual de triângulos, ângulos, semelhança, além de matemática básica (operações com números inteiros, regras de sinais, adição e subtração de inteiros, multiplicação e divisão com sinais — “jogo de sinais”).
Quero revisar com Mapas MentaisComo aplicar a desigualdade triangular
- Validar lados: dados três números positivos, verifique as três desigualdades.
- Encontrar intervalo do terceiro lado: com dois lados fixos, o terceiro deve ficar entre a diferença e a soma.
- Classificação: combinada com ângulos, ajuda a antecipar se o triângulo pode ser agudo, reto ou obtuso.
Exemplos resolvidos (passo a passo)
Exemplo 1 — Validar um trio de lados
Os comprimentos \(a=7\), \(b=10\) e \(c=18\) formam triângulo?
Ver solução
Exemplo 2 — Intervalo para o terceiro lado
Com \(a=6\) e \(b=9\), determine o intervalo de valores possíveis para \(c\).
Ver solução
Exemplo 3 — Problema com parâmetro
Os lados são \(x\), \(12\) e \(17\). Encontre o intervalo de \(x\) para existir triângulo.
Ver solução
eBook Gratuito de Fórmulas Matemáticas — Destaque
Baixe o PDF com fórmulas de geometria plana, triângulos e um apanhado de operações com números inteiros (regras de sinais) para não errar nas contas.
Baixar grátis agoraExercícios propostos (com toggle)
Escreva as contas uma abaixo da outra após o “=” para leitura confortável no celular.
1) Discursiva — Hastes de metal
Um técnico possui hastes de \(8\) cm e \(13\) cm. Qual o intervalo de comprimentos que a terceira haste \(x\) pode ter para montar um triângulo?
Ver solução
2) Múltipla escolha — Triângulo possível?
Quais das trincas podem ser lados de um triângulo?
- (4, 5, 10)
- (7, 8, 14)
- (6, 9, 14)
- (3, 4, 6)
Mostrar resposta
Gabarito: B, C e D.
3) Discursiva — Intervalo com variável
Os lados são \(5\), \(x\) e \(x+4\). Determine os valores de \(x\) para que o triângulo exista.
Ver solução
Links internos e produtos do blog
Conclusão
A Desigualdade Triangular é a condição de existência de qualquer triângulo. Use-a para validar medidas e para obter o intervalo possível do terceiro lado. Reforce o estudo com os artigos de ângulos — soma dos internos, soma dos externos e teorema do ângulo externo.
Próximo passo: baixe o eBook gratuito de Fórmulas e acompanhe a rota de estudos no ENEM Matemática.













