A parábola

A parábola: foco, diretriz, equações canônicas, propriedades e exemplos

A parábola: foco, diretriz e equações canônicas

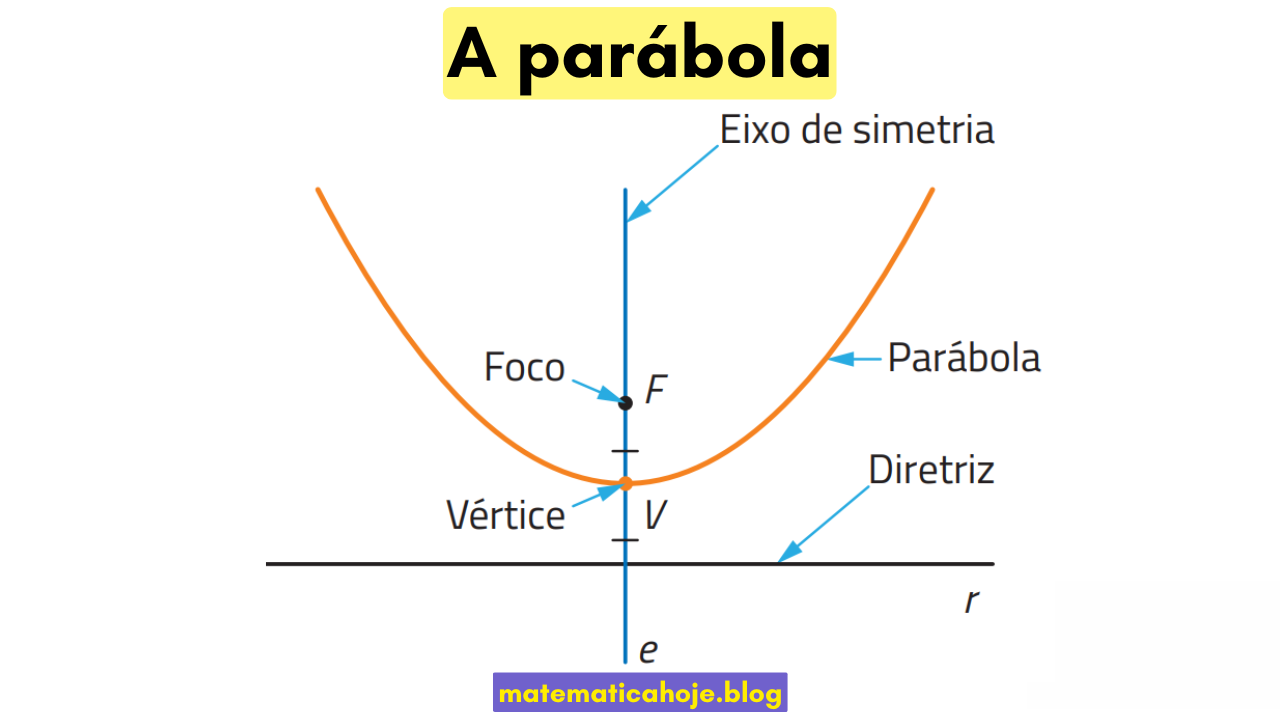
Em Geometria Analítica, parábola é o lugar geométrico dos pontos \(P\) do plano que estão à mesma distância de um ponto fixo \(F\) (foco) e de uma reta fixa \(r\) (diretriz). O ponto médio entre \(F\) e \(r\) é o vértice, e a reta perpendicular a \(r\) que passa por esse vértice é o eixo de simetria.

Diagrama de uma parábola com foco F, vértice V, eixo de simetria vertical, e a diretriz r.

Para o estudo funcional da parábola como gráfico de uma função quadrática, veja também: gráfico da quadrática, sinal da função e inequações produto.

1) Dedução da equação canônica \(x^2=4py\)

Considere foco \(F=(0,p)\) e diretriz \(y=-p\) (parábola abrindo para cima). Pela definição, a distância de \((x,y)\) ao foco é igual à distância à diretriz:

\[ \begin{aligned} \sqrt{(x-0)^2 + (y-p)^2} &= |y – (-p)|\\ \sqrt{x^2 + (y-p)^2} &= |y+p|\\ x^2 + (y-p)^2 &= (y+p)^2\\ x^2 + y^2 – 2py + p^2 &= y^2 + 2py + p^2\\ x^2 – 4py &= 0\\ \boxed{x^2 = 4py} \end{aligned} \]

Nessa forma, \(p\) é a distância do vértice ao foco (e também do vértice à diretriz). O segmento que passa pelo foco e é paralelo à diretriz, cortando a parábola, tem comprimento \(|4p|\) e chama-se latus rectum.

2) Outras formas canônicas e translações

Eixo horizontal (abrindo para a direita/esquerda): \(\boxed{y^2=4px}\) com foco \((p,0)\) e diretriz \(x=-p\).
Translações: se o vértice é \((h,k)\), \[ \boxed{(x-h)^2 = 4p(y-k)} \quad \text{ou} \quad \boxed{(y-k)^2 = 4p(x-h)}. \]
Relação com a forma funcional: \(x^2=4py \iff y=\dfrac{x^2}{4p}\) (uma quadrática com eixo vertical).

3) Propriedades úteis

Eixo de simetria: a parábola é simétrica em relação à reta que passa pelo vértice e foco.
Reflexão: o raio que parte do foco e bate na parábola reflete paralelamente ao eixo (e vice-versa). É a base dos espelhos parabólicos.
Tangente em \(x^2=4py\): no ponto \((x_1,y_1)\) da parábola, a equação da tangente pode ser escrita como \[ \boxed{x\,x_1 = 2p\,(y+y_1)}. \] (Se preferir derivada: \(y=\tfrac{x^2}{4p}\Rightarrow y’=\tfrac{x}{2p}\) e use a forma ponto-inclinação.)
Latus rectum: para \(x^2=4py\), o segmento paralelo à diretriz que passa pelo foco tem comprimento \(|4p|\) e extremos \((2p,\,p)\) e \((-2p,\,p)\).

4) Exemplos resolvidos (contas uma embaixo da outra)

Exemplo 1 — Identificar foco e diretriz de \(y=\dfrac{x^2}{8}\)

Compare com \(x^2=4py\).

\[ \begin{aligned} y &= \frac{x^2}{8}\\ x^2 &= 8y\\ 4p &= 8\\ p &= 2\\ \text{Foco} &= (0,2)\\ \text{Diretriz} &: y=-2 \end{aligned} \]

Exemplo 2 — Transladada: \((x-3)^2=12(y+1)\)

Compare com \((x-h)^2=4p(y-k)\).

\[ \begin{aligned} (x-3)^2 &= 12(y+1)\\ 4p &= 12\\ p &= 3\\ (h,k) &= (3,-1)\\ \text{Vértice} &= (3,-1)\\ \text{Foco} &= (3,\,-1+3) = (3,2)\\ \text{Diretriz} &: y = -1 – 3 = -4\\ \text{Eixo} &: x=3 \end{aligned} \]

Exemplo 3 — Eixo horizontal: \(y^2=4x\)

\[ \begin{aligned} y^2 &= 4x\\ 4p &= 4\\ p &= 1\\ \text{Foco} &= (1,0)\\ \text{Diretriz} &: x=-1\\ \text{Abertura} &: \text{para a direita} \end{aligned} \]

5) Como esboçar rapidamente

Coloque a equação em uma das canônicas (\(x^2=4py\), \(y^2=4px\), ou suas versões transladadas).
Leia \(p\), marque o vértice, o foco e a diretriz.
Use o eixo de simetria e alguns pontos (por exemplo, sobre o latus rectum) para guiar a curva.
Lembre: se \(p>0\) a abertura é para cima/direita; se \(p<0\), para baixo/esquerda.

6) Relação com a função quadrática

Toda parábola com eixo paralelo a \(y\) pode ser escrita como \(y=ax^2+bx+c\) (ver função quadrática). A passagem entre \(x^2=4py\) e a forma funcional é imediata: \[ x^2 = 4py \iff y = \frac{x^2}{4p}. \] Para translações, use \((x-h)^2=4p(y-k)\Rightarrow y = \dfrac{(x-h)^2}{4p}+k\).

7) Continue estudando

Função quadrática (guia completo) Gráfico da quadrática Função modular (|x|) Inequações quociente Inequações produto Sinal da função

Relacionadas

Valor máximo e mínimo de uma função quadrática

Zeros ou Raiz de uma Função Quadrática

Função Quadrática: Pontos notáveis da parábola

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.