Área de Triângulo — fórmulas com exemplos passo a passo
Guia prático de Geometria Plana com linkagens internas para continuar estudando.
Resumo das fórmulas
1) Triângulo qualquer (ou obtusângulo)
Fórmula: \( A=\frac{b\cdot h}{2} \). Use a altura perpendicular à base; em obtusângulos, ela pode cair fora do triângulo.
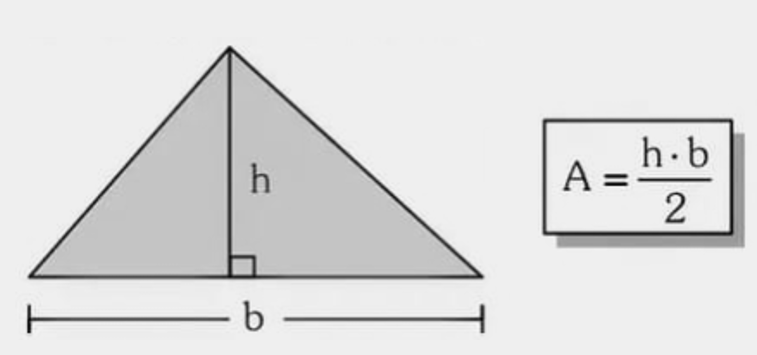
Exemplo 1 — Um canteiro triangular será revestido com mantas. O lado apoiado no muro mede \(b=10\,\text{cm}\) (em escala) e a distância perpendicular até o vértice é \(h=6\,\text{cm}\). Qual é a área do canteiro (na escala), em cm²?
Ver solução passo a passo
- \( A=\frac{b\cdot h}{2} \).
- \( A=\frac{10\cdot6}{2}=\frac{60}{2} \).
- \( \boxed{A=30\,\text{cm}^2} \).
Exemplo 2 — O desenho de um telhado obtusângulo mostra a base \(b=12\,\text{cm}\) e a altura projetada fora da peça \(h=5{,}2\,\text{cm}\). Qual a área da telha representada?
Ver solução passo a passo
- \( A=\frac{12\cdot5{,}2}{2}=\frac{62{,}4}{2} \).
- \( \boxed{A=31{,}2\,\text{cm}^2} \).
2) Triângulo retângulo (catetos)
Fórmula: \( A=\frac{cat_1\cdot cat_2}{2} \). Relembre o Teorema de Pitágoras.
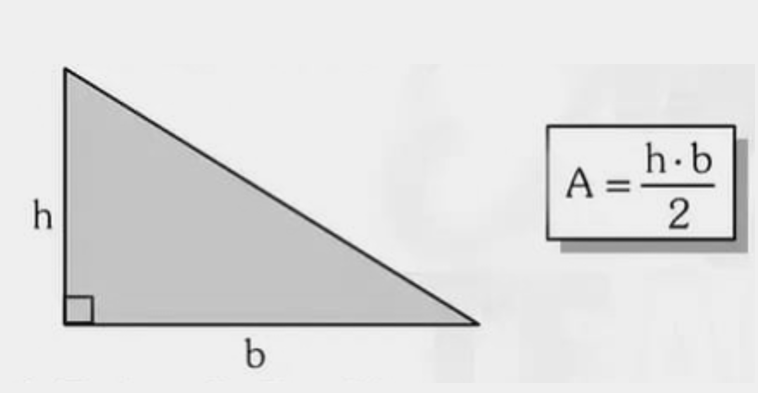
Exemplo 1 — Uma bandeira triangular retângula será costurada. Os lados perpendiculares medem \(9\,\text{cm}\) e \(12\,\text{cm}\). Qual é a área do tecido necessário?
Ver solução passo a passo
- \( A=\frac{9\cdot12}{2} \).
- \( A=\frac{108}{2}=54 \Rightarrow \boxed{54\,\text{cm}^2} \).
Exemplo 2 — Uma placa de sinalização tem formato de triângulo retângulo com catetos \(5\,\text{cm}\) e \(7\,\text{cm}\). Qual a área frontal da placa?
Ver solução passo a passo
- \( A=\frac{5\cdot7}{2}=\frac{35}{2} \).
- \( \boxed{A=17{,}5\,\text{cm}^2} \).
3) Triângulo equilátero
Com o lado: \( A=\frac{L^{2}\sqrt{3}}{4} \)
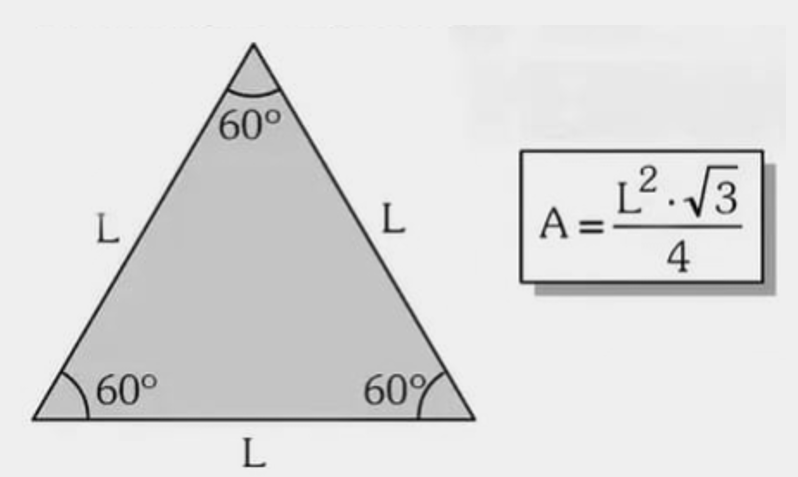
Exemplo 1 — Um mosaico usa peças equiláteras de lado \(8\,\text{cm}\). Qual a área de uma peça para estimar a quantidade de cerâmica?
Ver solução passo a passo
- \( A=\frac{8^{2}\sqrt{3}}{4}=\frac{64\sqrt{3}}{4}=16\sqrt{3} \).
- \( \boxed{A\approx 27{,}71\,\text{cm}^2} \).
Exemplo 2 — Em um logotipo, o triângulo equilátero tem lado \(12\,\text{cm}\). Qual é a área da figura impressa?
Ver solução passo a passo
- \( A=\frac{12^{2}\sqrt{3}}{4}=36\sqrt{3} \).
- \( \boxed{A\approx 62{,}35\,\text{cm}^2} \).
Com a altura: \( A=\frac{h^{2}\sqrt{3}}{3} \)
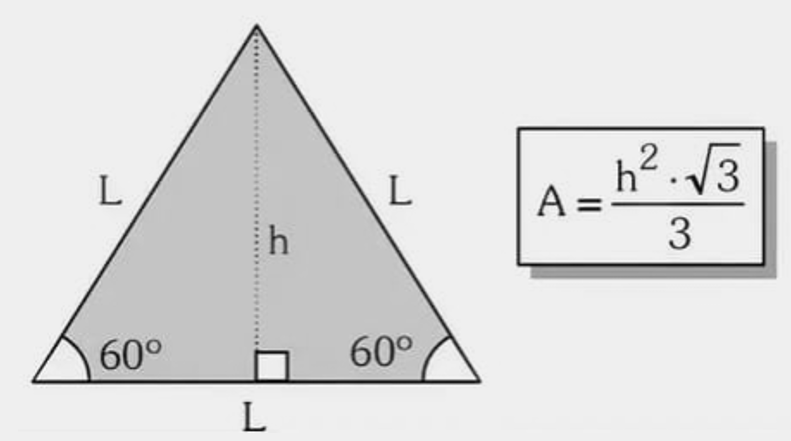
Exemplo 3 — Uma trave forma um triângulo equilátero cuja altura medida com trena é \(h\approx 8{,}66\,\text{cm}\) (em escala). Qual a área correspondente?
Ver solução passo a passo
- \( A=\frac{(8{,}66)^{2}\sqrt{3}}{3} \).
- \( \boxed{A\approx 43{,}30\,\text{cm}^2} \).
Exemplo 4 — Uma peça de artesanato é um equilátero com altura \(h=5{,}5\,\text{cm}\). Qual é a área de pintura dessa peça?
Ver solução passo a passo
- \( A=\frac{5{,}5^{2}\sqrt{3}}{3}=\frac{30{,}25\sqrt{3}}{3} \).
- \( \boxed{A\approx 17{,}46\,\text{cm}^2} \).
4) Dois lados e o ângulo compreendido
Fórmula: \( A=\frac{ab\sin\theta}{2} \). Veja Lei dos Senos e Lei dos Cossenos.
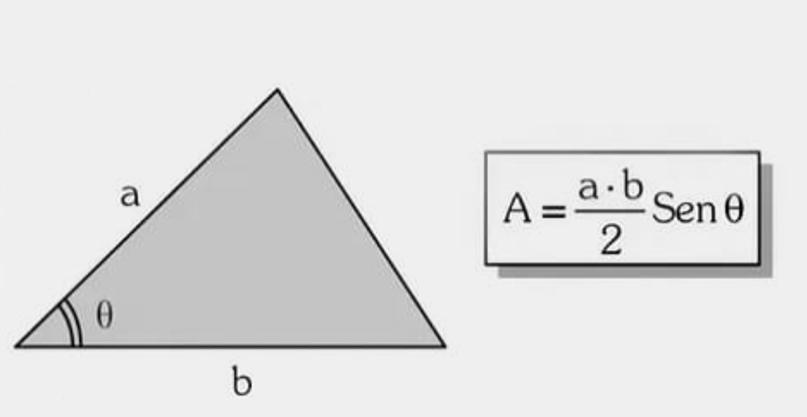
Exemplo 1 — Em um lote urbano, dois lados medem \(7\,\text{m}\) e \(10\,\text{m}\) e formam ângulo de \(30^\circ\). Qual a área aproximada desse triângulo de terreno?
Ver solução passo a passo
- \( \sin 30^\circ=0{,}5 \).
- \( A=\frac{7\cdot10\cdot0{,}5}{2}=\frac{35}{2} \).
- \( \boxed{A=17{,}5\,\text{u.a.}^2} \).
Exemplo 2 — Um suporte metálico tem barras de \(12\,\text{cm}\) e \(9\,\text{cm}\) formando \(60^\circ\). Qual a área ocupada pelo suporte?
Ver solução passo a passo
- \( \sin 60^\circ=\frac{\sqrt{3}}{2}\approx0{,}8660 \).
- \( A\approx \frac{12\cdot9\cdot0{,}8660}{2}\approx 46{,}77 \).
- \( \boxed{A\approx 46{,}77\,\text{u.a.}^2} \).
5) Três lados conhecidos — Fórmula de Heron
Semiperímetro: \( p=\frac{a+b+c}{2} \). Área: \( A=\sqrt{\,p(p-a)(p-b)(p-c)\,} \).
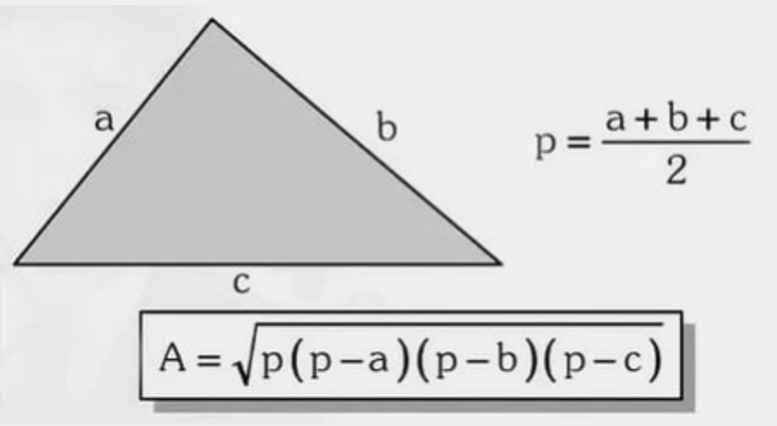
Exemplo 1 — Um terreno triangular possui lados de \(7\,\text{m}\), \(8\,\text{m}\) e \(9\,\text{m}\). Qual é a área aproximada para estimar a quantidade de grama?
Ver solução passo a passo
- \( p=\frac{7+8+9}{2}=12 \).
- \( A=\sqrt{12\cdot5\cdot4\cdot3}=\sqrt{720} \).
- \( \boxed{A\approx 26{,}83} \).
Exemplo 2 — Um vitral tem contorno triangular com lados \(13\,\text{cm}\), \(14\,\text{cm}\) e \(15\,\text{cm}\). Qual a área de vidro necessária?
Ver solução passo a passo
- \( p=\frac{13+14+15}{2}=21 \).
- \( A=\sqrt{21\cdot8\cdot7\cdot6}=\sqrt{7056} \).
- \( \boxed{A=84} \).
6) Retângulo com altura na hipotenusa
Se a altura à hipotenusa divide-a em segmentos \(m\) e \(n\), então \( \mathbf{A=m\cdot n} \).
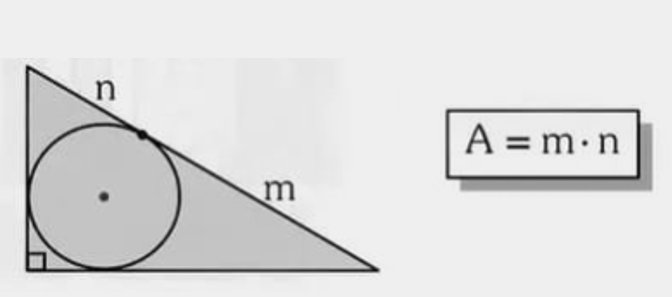
Exemplo 1 — Em uma rampa, a altura até a hipotenusa divide-a em segmentos \(m=6\,\text{cm}\) e \(n=8\,\text{cm}\). Qual a área do triângulo formado pela rampa e o chão?
Ver solução passo a passo
- \( A=m\cdot n=6\cdot8 \).
- \( \boxed{A=48} \).
Exemplo 2 — Um suporte retangular tem a hipotenusa seccionada pela altura em \(m=3{,}5\,\text{cm}\) e \(n=7\,\text{cm}\). Qual é a área da peça?
Ver solução passo a passo
- \( A=3{,}5\cdot7 \).
- \( \boxed{A=24{,}5} \).
7) Usando o raio da circunferência inscrita (inrário)
\( A=p\cdot r \), onde \(p\) é o semiperímetro e \(r\) o inrário. Veja pontos notáveis.
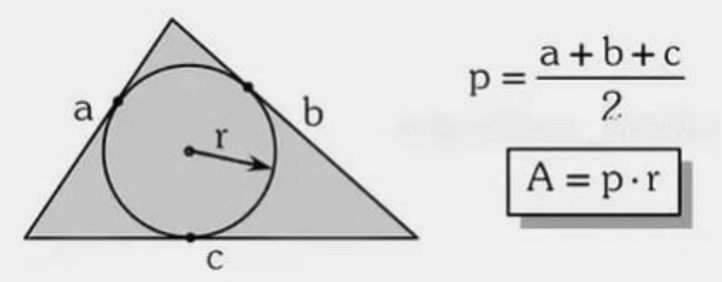
Exemplo 1 — Para demarcar um símbolo no piso, deseja-se pintar o triângulo cujo semiperímetro é \(p=21\) e o círculo inscrito tem raio \(r=4\). Qual a área a ser pintada?
Ver solução passo a passo
- \( A=p\cdot r=21\cdot4 \).
- \( \boxed{A=84} \).
Exemplo 2 — Um triângulo retângulo \(6\!-\!8\!-\!10\) será serigrafado; sabendo que \(p=12\) e \(r=2\), qual a área da impressão?
Ver solução passo a passo
- \( A=12\cdot2 \).
- \( \boxed{A=24} \).
8) Usando o raio da circunferência circunscrita (circunrádio)
Fórmula: \( A=\frac{abc}{4R} \).
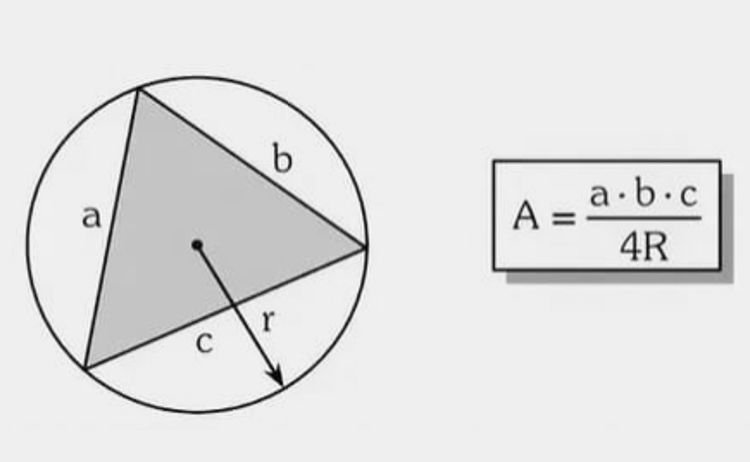
Exemplo 1 — Uma peça triangular \(3\!-\!4\!-\!5\) será recortada a partir de um disco de raio \(R=\frac{5}{2}\). Qual a área da peça?
Ver solução passo a passo
- \( A=\frac{3\cdot4\cdot5}{4\cdot2{,}5}=\frac{60}{10} \).
- \( \boxed{A=6} \).
Exemplo 2 — Um pingente em forma de equilátero tem lado \(10\,\text{cm}\) e é montado dentro de um aro circular de raio \(R=\dfrac{10}{\sqrt3}\). Qual a área do triângulo do pingente?
Ver solução passo a passo
- \( A=\frac{10\cdot10\cdot10}{4\cdot(10/\sqrt3)}=\frac{100\sqrt3}{4} \).
- \( \boxed{A=25\sqrt3\approx 43{,}30} \).