Área do Losango

O losango é um quadrilátero com os quatro lados congruentes. Suas diagonais são perpendiculares e bissetam os ângulos. Abaixo estão as principais fórmulas de área e exemplos práticos.

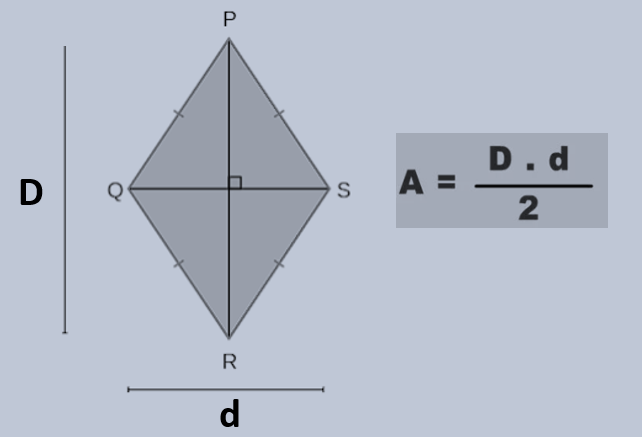
Losango com diagonais D e d e fórmula A = D·d/2 — Relação principal: \( \displaystyle A=\frac{D\cdot d}{2}\), onde \(D\) e \(d\) são as diagonais.

Reforce a base em: Área de Triângulo, Área do Trapézio, Lei dos Senos e Lei dos Cossenos.

Fórmulas da área do losango

\[ \textbf{Produto das diagonais:}\quad \boxed{A=\frac{D\cdot d}{2}} \]

\[ \textbf{Base × altura (paralelogramo):}\quad A=b\cdot h \]

\[ \textbf{Pelo lado e ângulo interno:}\quad A=\ell^{2}\,\sin\theta \]

Observação: em \(A=b\cdot h\), \(b\) é um lado tomado como base e \(h\) é a distância perpendicular entre lados paralelos.

\[ \textbf{Perímetro:}\quad P=4\ell \]

\[ \textbf{Relação lado–diagonais:}\quad \ell^2=\left(\frac{D}{2}\right)^2+\left(\frac{d}{2}\right)^2 \]

Exemplos resolvidos (situação-problema)

Área por diagonais

Uma placa de sinalização tem formato de losango com diagonais medidas em obra.

Dados: \(D=24\,\text{cm}\) e \(d=10\,\text{cm}\).

Pergunta: qual é a área da placa?

Ver solução

\[ \begin{aligned} A&=\frac{D\cdot d}{2}\\ &=\frac{24\cdot 10}{2}\\ &=\boxed{120\ \text{cm}^2} \end{aligned} \]

Área por lado e ângulo

Um azulejo em forma de losango (lados congruentes) será produzido com um ângulo interno definido pelo designer.

Dados: \(\ell=12\,\text{cm}\) e \(\theta=40^\circ\).

Pergunta: qual é a área do azulejo?

Ver solução

\[ \begin{aligned} A&=\ell^2\sin\theta\\ &=12^2\cdot \sin 40^\circ\\ &=144\cdot 0{,}642787\ldots\\ &\approx \boxed{92{,}6\ \text{cm}^2} \end{aligned} \]

Base × altura

Uma peça de tecido em losango será cortada a partir de um rolo, com a altura medida entre lados paralelos.

Dados: Base \(b=8\,\text{m}\) e altura \(h=5\,\text{m}\).

Pergunta: qual é a área do tecido?

Ver solução

\[ \begin{aligned} A&=b\cdot h\\ &=8\cdot 5\\ &=\boxed{40\ \text{m}^2} \end{aligned} \]

Perímetro + diagonal ⇒ outra diagonal e área

Um emblema tem perímetro conhecido e apenas a diagonal menor medida no protótipo.

Dados: \(P=40\,\text{cm}\Rightarrow \ell=10\,\text{cm}\); diagonal menor \(d=10\,\text{cm}\).

Pergunta: determine a outra diagonal \(D\) e a área.

Ver solução

\[ \begin{aligned} \ell^2&=\left(\frac{D}{2}\right)^2+\left(\frac{d}{2}\right)^2\\ 10^2&=\left(\frac{D}{2}\right)^2+\left(\frac{10}{2}\right)^2\\ 100&=\left(\frac{D}{2}\right)^2+25\\ \left(\frac{D}{2}\right)^2&=75\\ \frac{D}{2}&=\sqrt{75}\\ D&=2\sqrt{75}\approx 17{,}32\ \text{cm} \end{aligned} \] \[ \begin{aligned} A&=\frac{D\cdot d}{2}\\ &\approx \frac{17{,}32\cdot 10}{2}\\ &\approx \boxed{86{,}6\ \text{cm}^2} \end{aligned} \]

Erros comuns (e como evitar)

Confundir diagonais com lados. A fórmula \(A=\dfrac{D\,d}{2}\) usa diagonais, não os lados.

Usar \(\ell^2\sin\theta\) com ângulo externo. O \(\theta\) é o ângulo interno do losango.

Altura ≠ lado inclinado. Em \(A=b\cdot h\), \(h\) é a distância perpendicular entre lados paralelos.

Exercícios propostos

Diagonais em metros

Um piso decorativo foi desenhado como losango e as duas diagonais foram levantadas no local.

Dados: \(D=3{,}2\,\text{m}\) e \(d=1{,}5\,\text{m}\).

Calcule a área.

Ver gabarito

\[ A=\frac{3{,}2\cdot 1{,}5}{2}= \frac{4{,}8}{2}= \boxed{2{,}4\ \text{m}^2} \]

Lado e ângulo

Um azulejo losangular deve manter o ângulo interno proposto para preservar o design.

Dados: \(\ell=9\,\text{cm}\) e \(\theta=60^\circ\).

Calcule a área.

Ver gabarito

\[ A=\ell^2\sin 60^\circ= 81\cdot \frac{\sqrt{3}}{2} \approx \boxed{70{,}1\ \text{cm}^2} \]

Base × altura

Na confecção de bandeiras, a faixa central é um losango com base e altura já definidas.

Dados: \(b=25\,\text{cm}\) e \(h=14\,\text{cm}\).

Encontre a área.

Ver gabarito

\[ A=b\cdot h=25\cdot 14=\boxed{350\ \text{cm}^2} \]

Continue estudando

• Área de Triângulo — base–altura, 2 lados + ângulo e Heron.

• Área do Trapézio — fórmula, exemplos e exercícios.

• Triângulos — tipos e propriedades — propriedades úteis ao decompor figuras.

Área do Losango

Área do Losango

Fórmulas da área do losango

Exemplos resolvidos (situação-problema)

Área por diagonais

Área por lado e ângulo

Base × altura

Perímetro + diagonal ⇒ outra diagonal e área

Erros comuns (e como evitar)

Exercícios propostos

Diagonais em metros

Lado e ângulo

Base × altura

Continue estudando

Materiais do Matemática Hoje

Relações Métricas no Triângulo Retângulo

Área do Quadrado

Área do Circulo

"Artigo escrito por"

Adriano Rocha

Nos ajude compartilhando esse post 😉

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Circunferência: Raio, Diâmetro e Cordas

Comprimento da Circunferência

Área do Quadrado

Áreas do Retângulo

Área do Setor Circular

Área do Circulo

📘 Baixe Grátis o eBook de Fórmulas Matemática

📘 Mapas Mentais

📚 10 E-books de Matemática

Questões

Conteúdo

Banca