Ao estudar funções, especialmente no cálculo e no ensino médio, é essencial compreender o comportamento do gráfico nos extremos e em pontos críticos. Dois conceitos centrais nesse estudo são as assíntotas horizontais e assíntotas verticais. Elas indicam o comportamento de uma função quando \( x \) tende a valores infinitos ou a pontos onde a função não está definida.
📌 O que são assíntotas?
vAssíntotas são retas que o gráfico de uma função se aproxima, mas nunca toca completamente, exceto, talvez, em pontos isolados.
- Horizontais: descrevem o comportamento de \( f(x) \) quando \( x \to +\infty \) ou \( x \to -\infty \).
- Verticais: descrevem o comportamento de \( f(x) \) quando \( x \to a \), e \( f(x) \) tende ao infinito (positivo ou negativo).
🟨 Assíntota Horizontal
✅ Definição:
Dizemos que a reta \( y = b \), com \( b \in \mathbb{R} \), é uma assíntota horizontal do gráfico de uma função \( f \) se, pelo menos uma das seguintes condições for satisfeita:
(i) \( \lim_{x \to +\infty} f(x) = b \)
(ii) \( \lim_{x \to -\infty} f(x) = b \)
🔍 Exemplo:
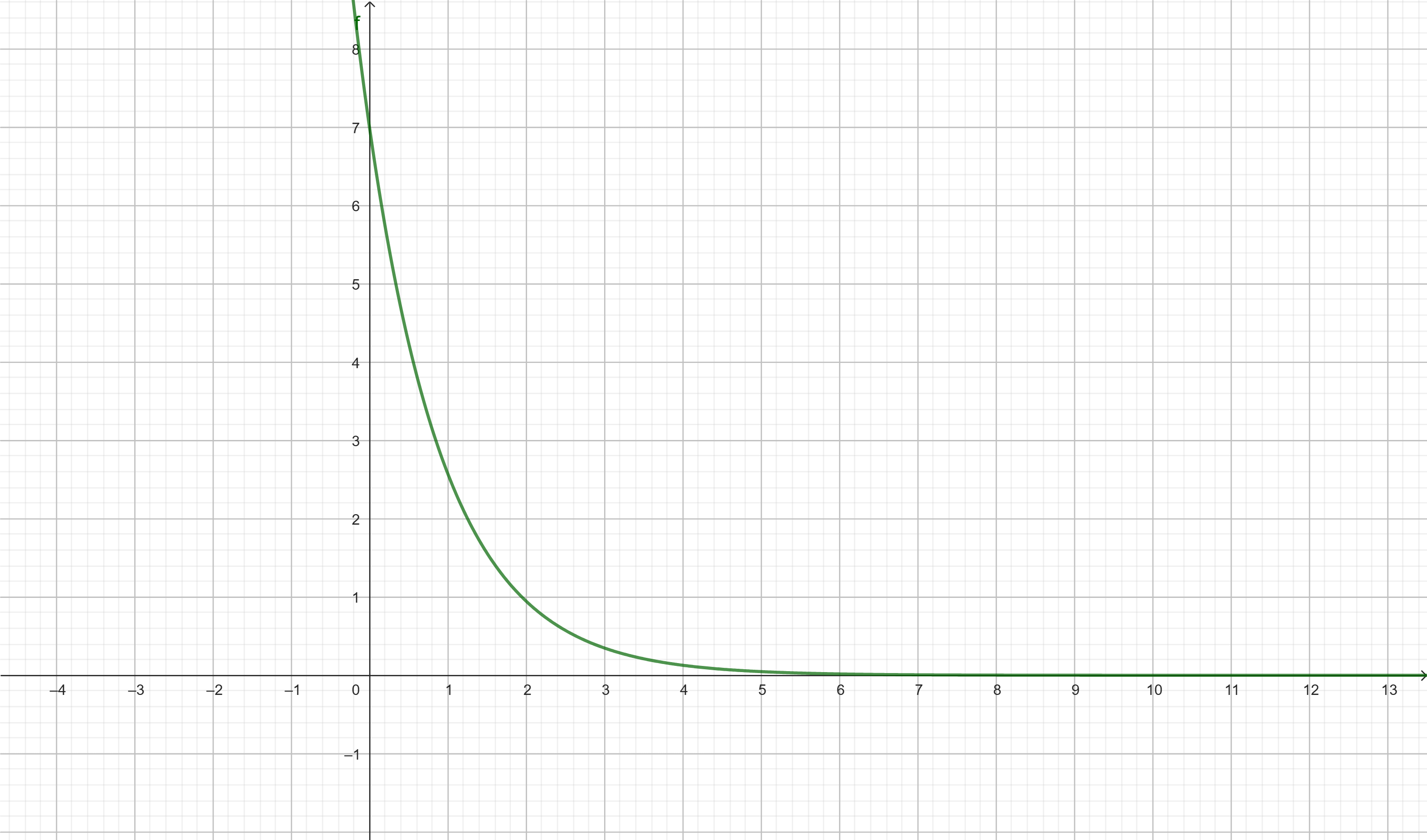
Seja \( f(x) = 7e^{-x} \). Como:
\( \lim_{x \to +\infty} 7e^{-x} = 0 \)
Então, a reta \( y = 0 \) é uma assíntota horizontal.
Essa função tende a zero à medida que \( x \to +\infty \), pois a parte exponencial se aproxima de zero:
\( f(100) = 7 \cdot e^{-100} \approx 0 \)
🟦 Assíntota Vertical
✅ Definição:
Dizemos que a reta \( x = a \) é uma assíntota vertical do gráfico de uma função \( f \) se, pelo menos uma das condições abaixo for satisfeita:
(i) \( \lim_{x \to a^+} f(x) = +\infty \)
(ii) \( \lim_{x \to a^+} f(x) = -\infty \)
(iii) \( \lim_{x \to a^-} f(x) = +\infty \)
(iv) \( \lim_{x \to a^-} f(x) = -\infty \)
🔍 Exemplo:
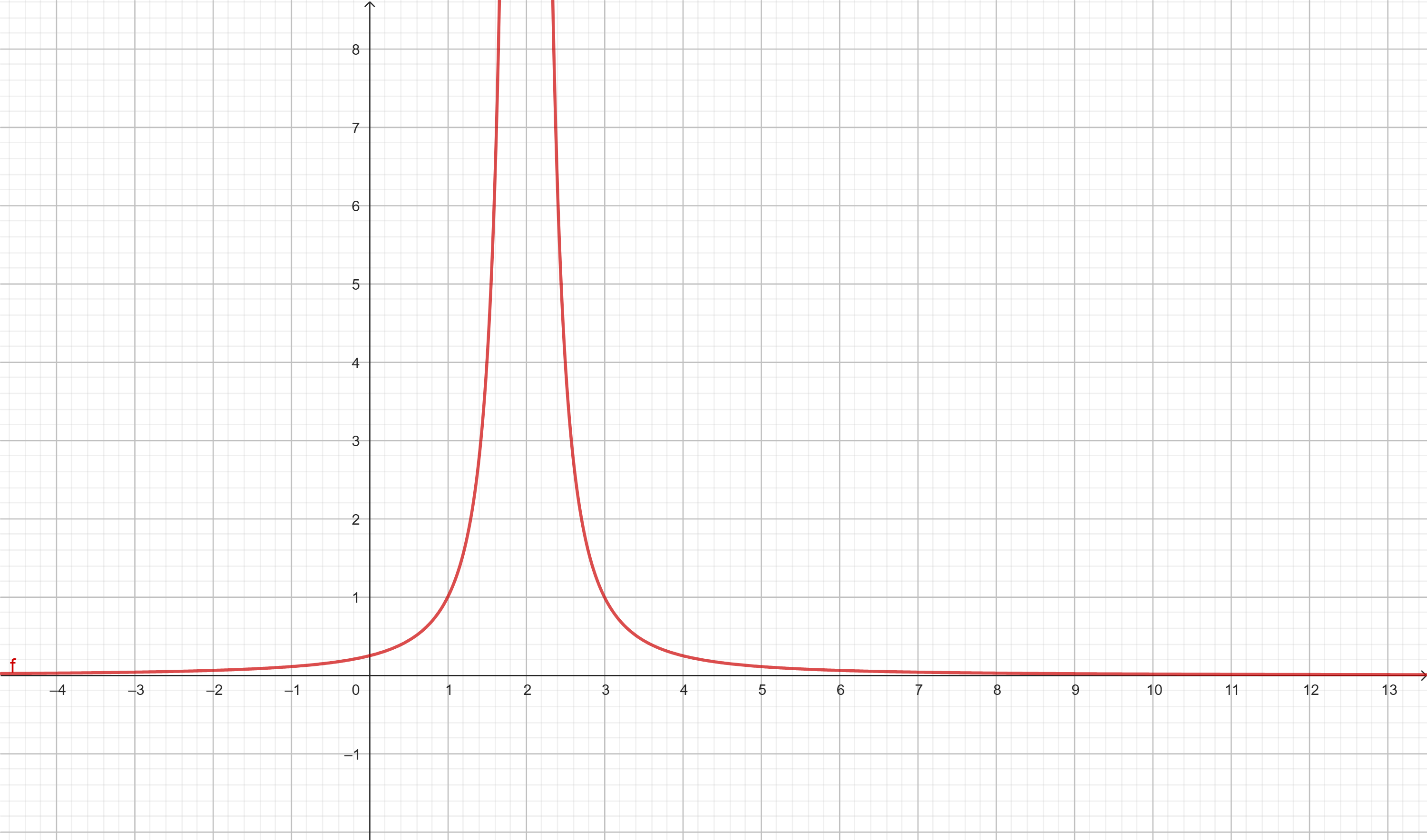
Considere a função:
\( f(x) = \frac{1}{(x – 2)^2} \)
O denominador se anula quando \( x = 2 \), o que torna a função indefinida nesse ponto.
Além disso:
\( \lim_{x \to 2^-} f(x) = +\infty \quad \text{e} \quad \lim_{x \to 2^+} f(x) = +\infty \)
Logo, a reta \( x = 2 \) é uma assíntota vertical.
🧠 Dica Rápida para Funções Racionais
Considere uma função racional do tipo:
\( f(x) = \frac{P(x)}{Q(x)} \)
onde \( P(x) \) e \( Q(x) \) são polinômios. Para encontrar assíntotas horizontais:
- Se \( \deg(P) < \deg(Q) \), então \( y = 0 \) é a assíntota horizontal.
- Se \( \deg(P) = \deg(Q) \), a assíntota horizontal é dada por: \( y = \frac{\text{coef. líder de } P(x)}{\text{coef. líder de } Q(x)} \)
- Se \( \deg(P) > \deg(Q) \), não há assíntota horizontal (pode haver assíntota oblíqua).
📌 Conclusão
As assíntotas são elementos fundamentais na análise gráfica de funções. Elas indicam limites de crescimento e comportamento extremo, sendo essenciais na construção de esboços precisos de gráficos.
Compreender assíntotas ajuda a interpretar limites, continuidade e o domínio das funções.
📝 Exercícios Resolvidos – Assíntotas Horizontais e Verticais
✅ Exercício 1 – Assíntota vertical
Enunciado:
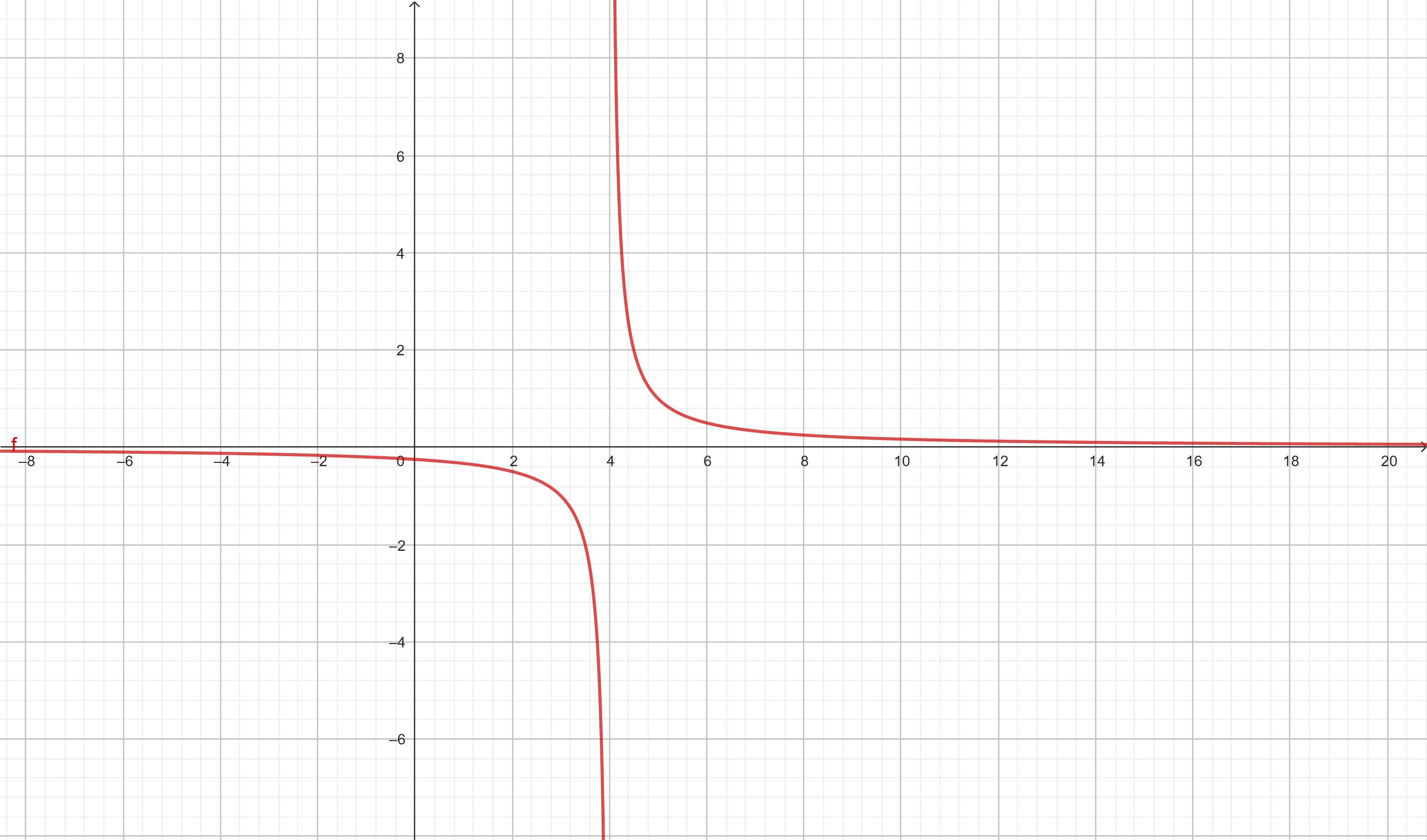
Determine a assíntota vertical da função:
\( f(x) = \frac{1}{x – 4} \)
Solução:
O denominador zera quando \( x = 4 \), o que gera uma discontinuidade do tipo infinito:
\( \lim_{x \to 4^-} f(x) = -\infty \quad \text{e} \quad \lim_{x \to 4^+} f(x) = +\infty \)
Assíntota vertical: \( x = 4 \)
✅ Exercício 2 – Assíntota horizontal
Enunciado:
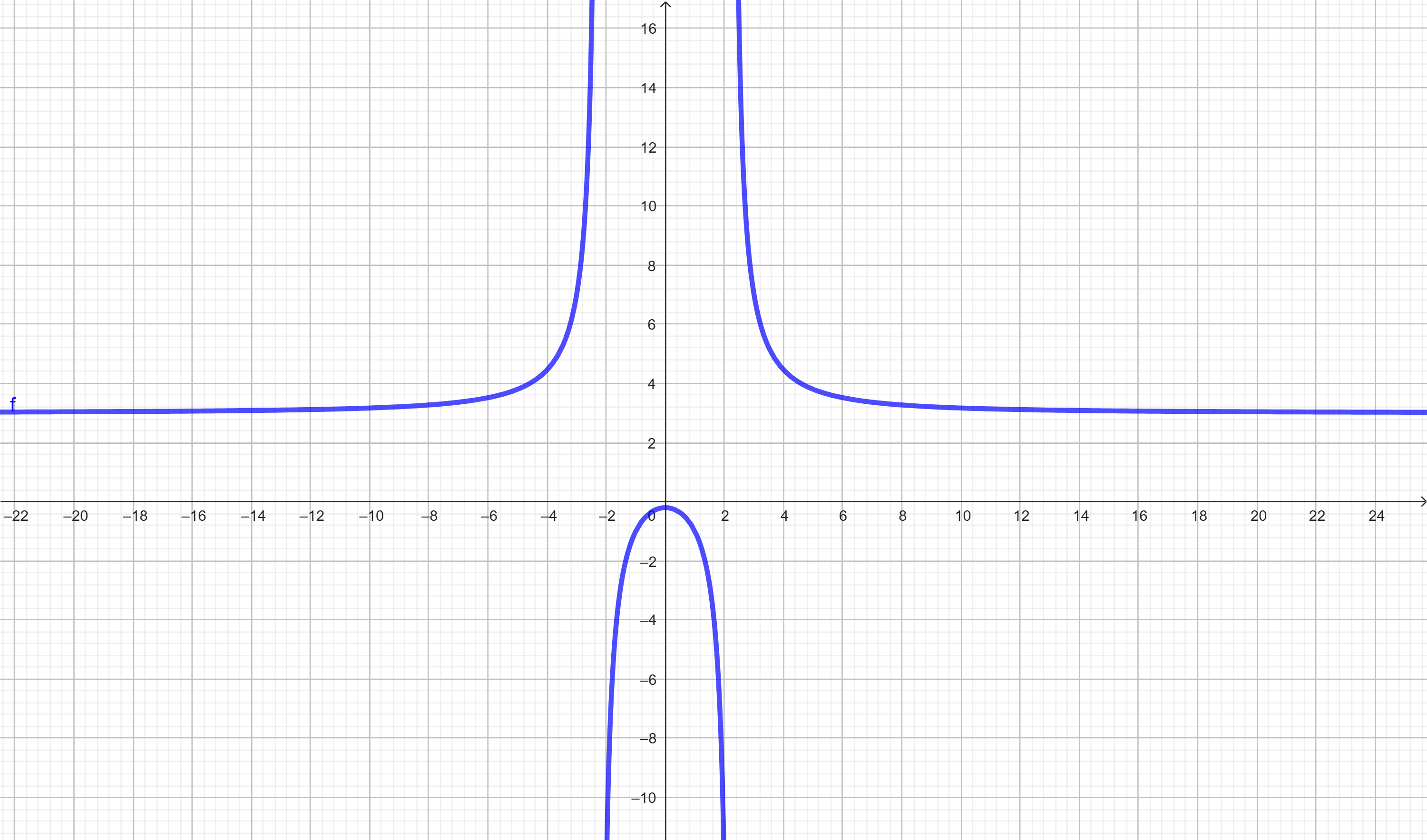
Encontre a assíntota horizontal da função:
\( f(x) = \frac{3x^2 + 1}{x^2 – 5} \)
Solução:
Os polinômios possuem mesmo grau (grau 2). Consideramos os coeficientes líderes:
\( \lim_{x \to \infty} f(x) = \frac{3}{1} = 3 \)
Assíntota horizontal: \( y = 3 \)
✅ Exercício 3 – Nenhuma assíntota horizontal
Enunciado:
A função abaixo possui assíntota horizontal? Justifique:
\( f(x) = \frac{x^3 + 2}{x + 1} \)
Solução:
Grau do numerador = 3
Grau do denominador = 1
Como o grau do numerador é maior, a função não possui assíntota horizontal.
Resposta: Não possui assíntota horizontal. (Pode ter assíntota oblíqua)
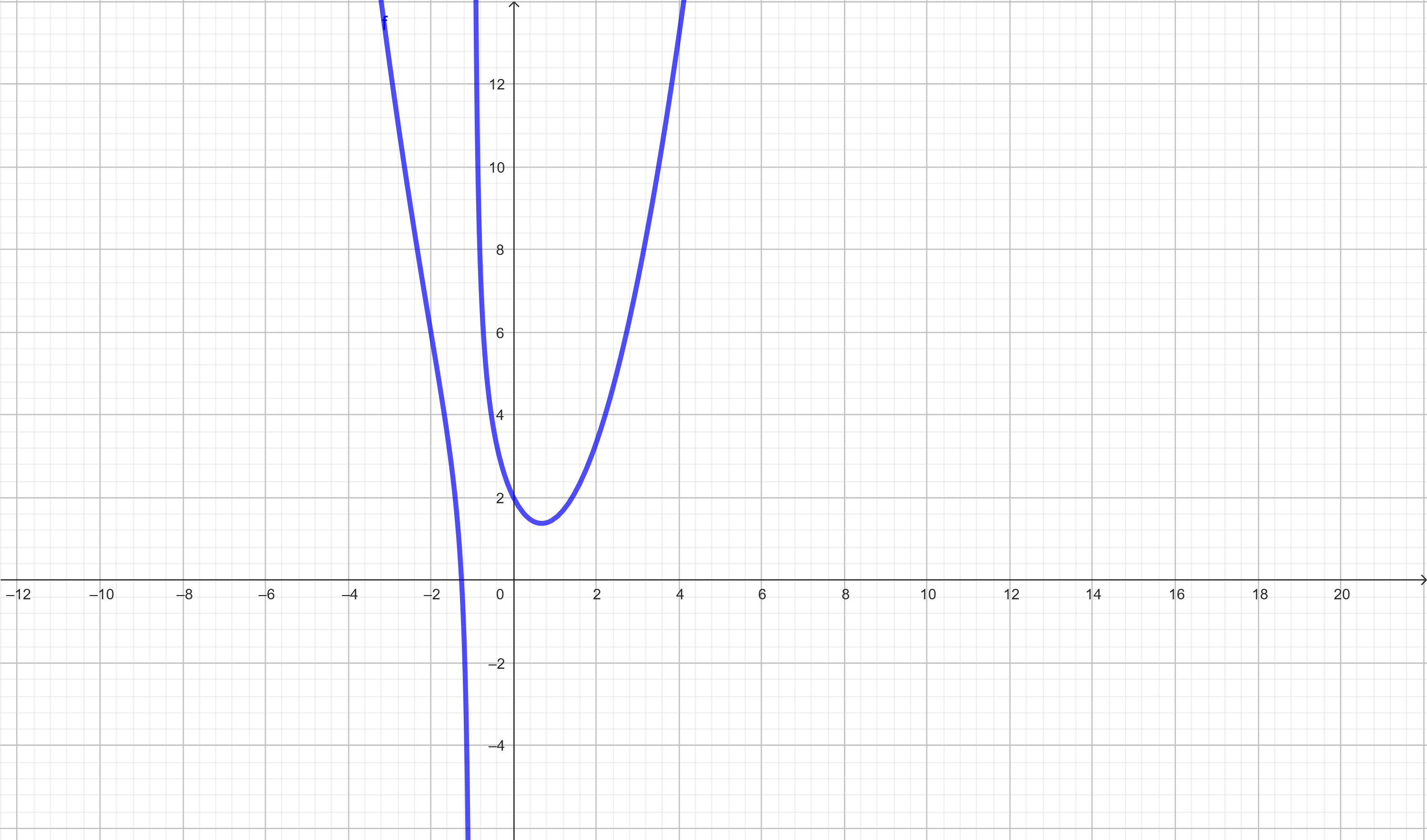
✅ Exercício 4 – Duas assíntotas verticais
Enunciado:
Determine as assíntotas verticais da função:
\( f(x) = \frac{1}{x^2 – 9} \)
Solução:
Fatorando o denominador: \( x^2 – 9 = (x – 3)(x + 3) \)
As raízes são \( x = 3 \) e \( x = -3 \)
Assíntotas verticais: \( x = 3 \) e \( x = -3 \)
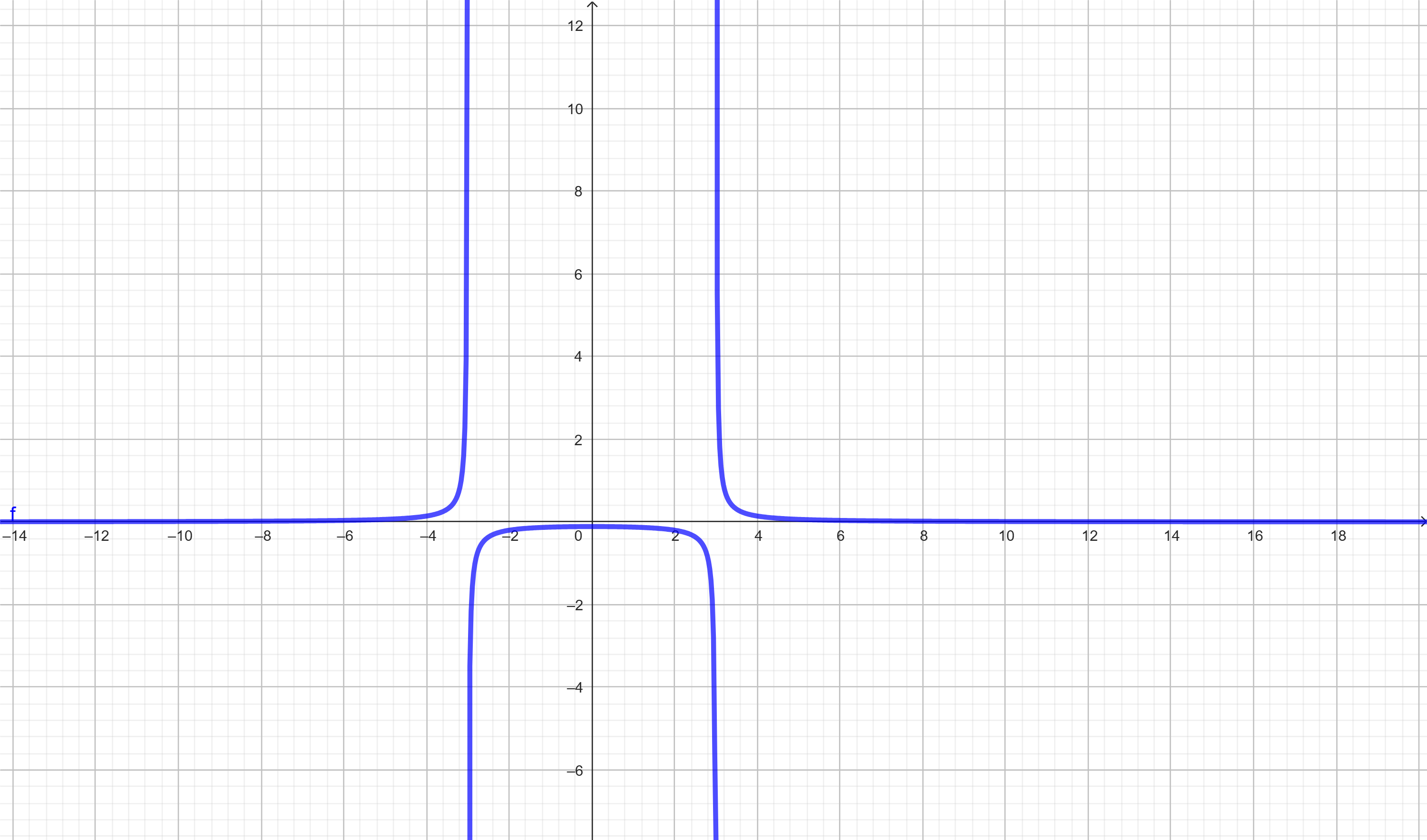
✅ Exercício 5 – Uma horizontal e uma vertical
Enunciado:
Encontre as assíntotas da função:
\( f(x) = \frac{2x + 1}{x – 1} \)
Solução:
Assíntota vertical:
O denominador zera em \( x = 1 \), logo:
\( x = 1 \) é uma assíntota vertical.
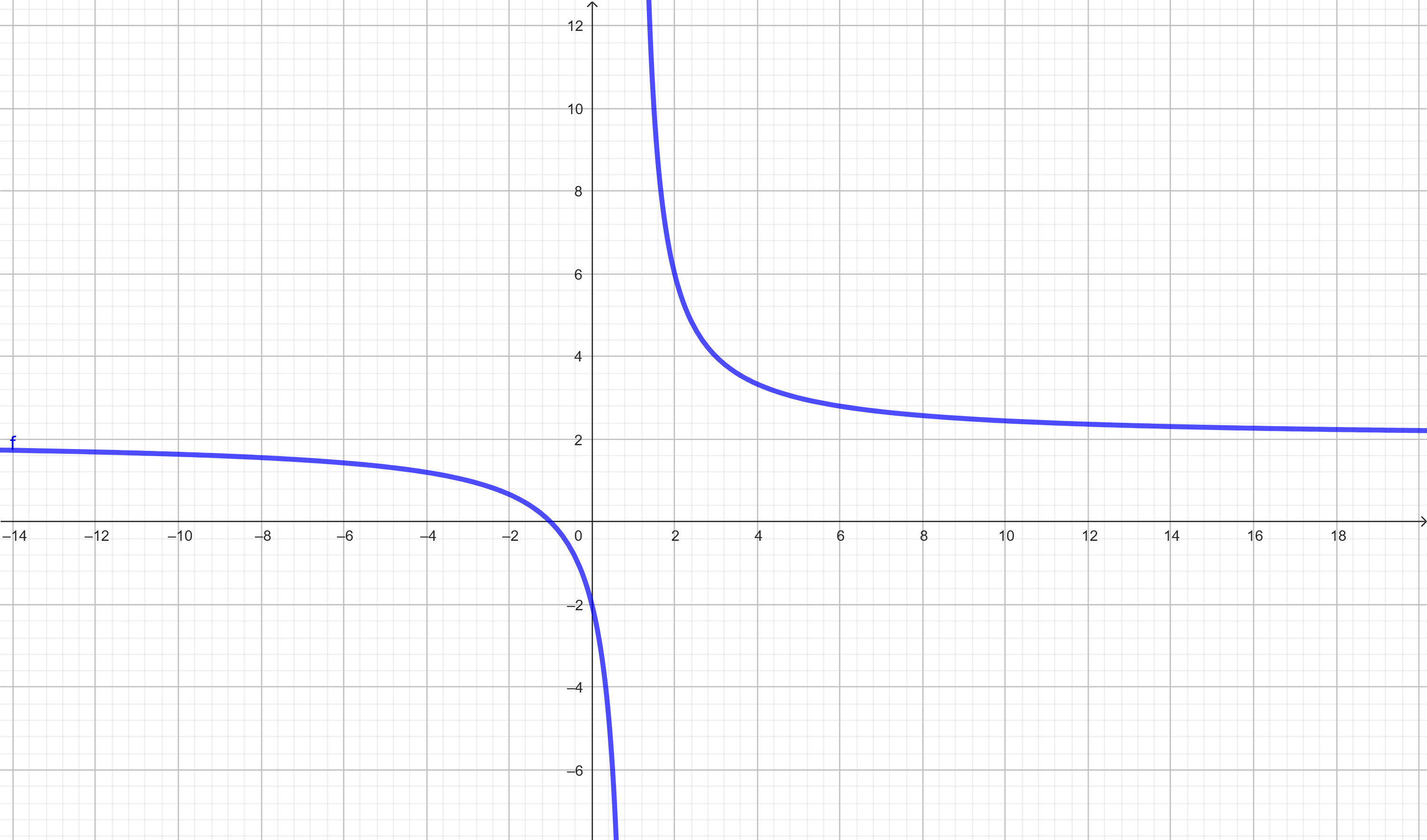Assíntota horizontal:
Os polinômios possuem grau 1. Usamos os coeficientes principais:\( \lim_{x \to \infty} f(x) = \frac{2}{1} = 2 \)
Resposta:
Assíntota vertical: \( x = 1 \)
Assíntota horizontal: \( y = 2 \)
Gostou do conteúdo? Compartilhe com seus colegas e continue explorando mais sobre funções no blog Matemática Hoje!
