O cilindro é uma figura geométrica tridimensional composta por duas bases circulares paralelas e uma superfície lateral curva. É uma das formas mais comuns em várias áreas, como engenharia, arquitetura e design. Neste artigo, vamos explorar como calcular a área da base, área lateral, área total e volume de um cilindro, além de abordar o conceito de cilindro equilátero e a planificação.
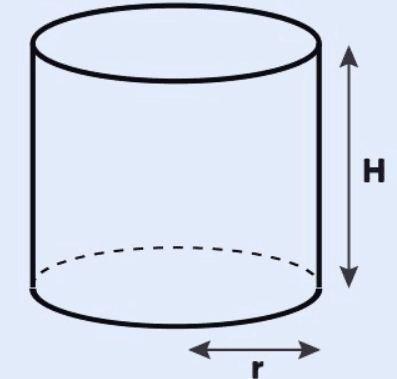
1. Área da Base
O cilindro possui duas bases circulares. Se ( r ) é o raio da base, a área de cada base é dada por:
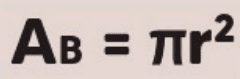
Essa é a fórmula clássica para a área de um círculo, onde π é uma constante aproximadamente igual a 3,1416.
2. Área Lateral
A área lateral de um cilindro é a área da superfície curva que conecta as duas bases. Para calculá-la, usamos a altura H do cilindro e o perímetro da base:

Aqui, 2πr é o comprimento da circunferência da base, que, multiplicado pela altura, dá a área lateral.
3. Área Total
A área total do cilindro é a soma da área lateral com as áreas das duas bases:
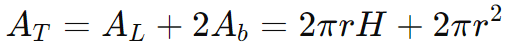
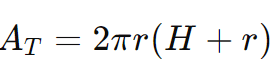

Essa fórmula representa a soma da área da superfície lateral com as duas áreas circulares das bases.
4. Volume
O volume do cilindro, que representa o espaço tridimensional ocupado pela figura, é dado pela multiplicação da área da base pela altura:
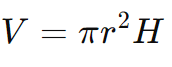

Essa fórmula mostra como o volume de um cilindro é diretamente proporcional ao quadrado do raio da base e à altura.
5. Cilindro Equilátero
Um cilindro é dito equilátero quando sua altura H é igual ao diâmetro da base, ou seja, H = 2r. Nesse caso, as fórmulas de área e volume podem ser ajustadas:
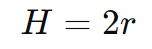
Substituindo na fórmula da área lateral e da área total:
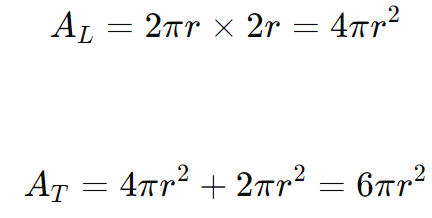
E o volume torna-se:
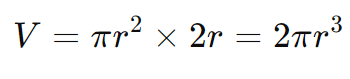

6. Planificação
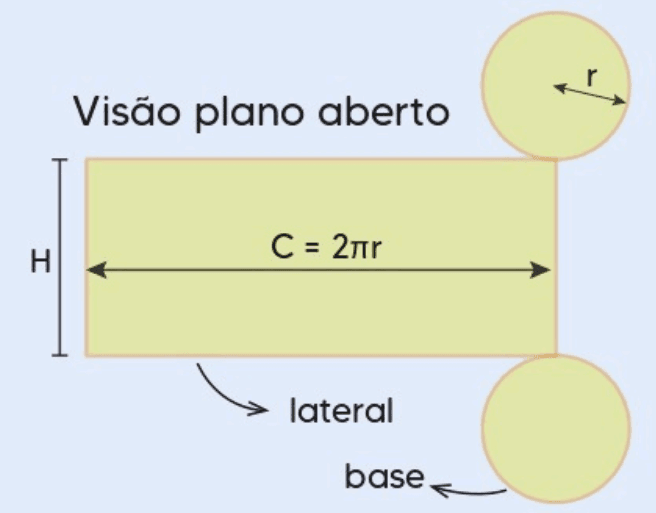
A planificação de um cilindro envolve desdobrar sua superfície lateral e as duas bases em um plano bidimensional. A superfície lateral se transforma em um retângulo, cujas dimensões são a altura H e o comprimento da circunferência da base 2πr. As duas bases, por sua vez, permanecem como dois círculos de raio r.
Conclusão
O cilindro é uma forma geométrica fundamental com aplicações práticas e teóricas vastas. Conhecer as fórmulas para calcular sua área da base, área lateral, área total e volume é essencial para resolver problemas relacionados a essa figura. O cilindro equilátero oferece uma variante interessante, enquanto a planificação facilita a visualização de sua estrutura em duas dimensões. Essas habilidades são úteis em diversas disciplinas, como matemática, física e engenharia, onde o entendimento das propriedades geométricas do cilindro é crucial.
Leia também
O Cubo: Propriedades e Fórmulas Essenciais
O Paralelepípedo: Propriedades e Fórmulas Essenciais
Pirâmides: Propriedades, Fórmulas e Aplicações
Tetraedro Regular: Propriedades, Fórmulas e Aplicações
Tronco de Pirâmide: Propriedades, Fórmulas e Proporções
Cilindro: Conceitos e Cálculos
Cone: Tudo o Que Você Precisa Saber
Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão